Чем отличается равномерное движение от равноускоренного

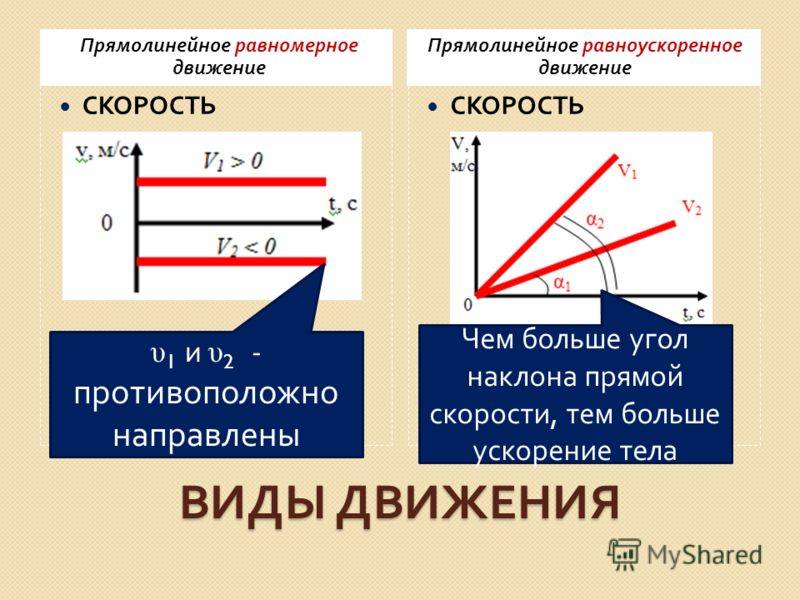
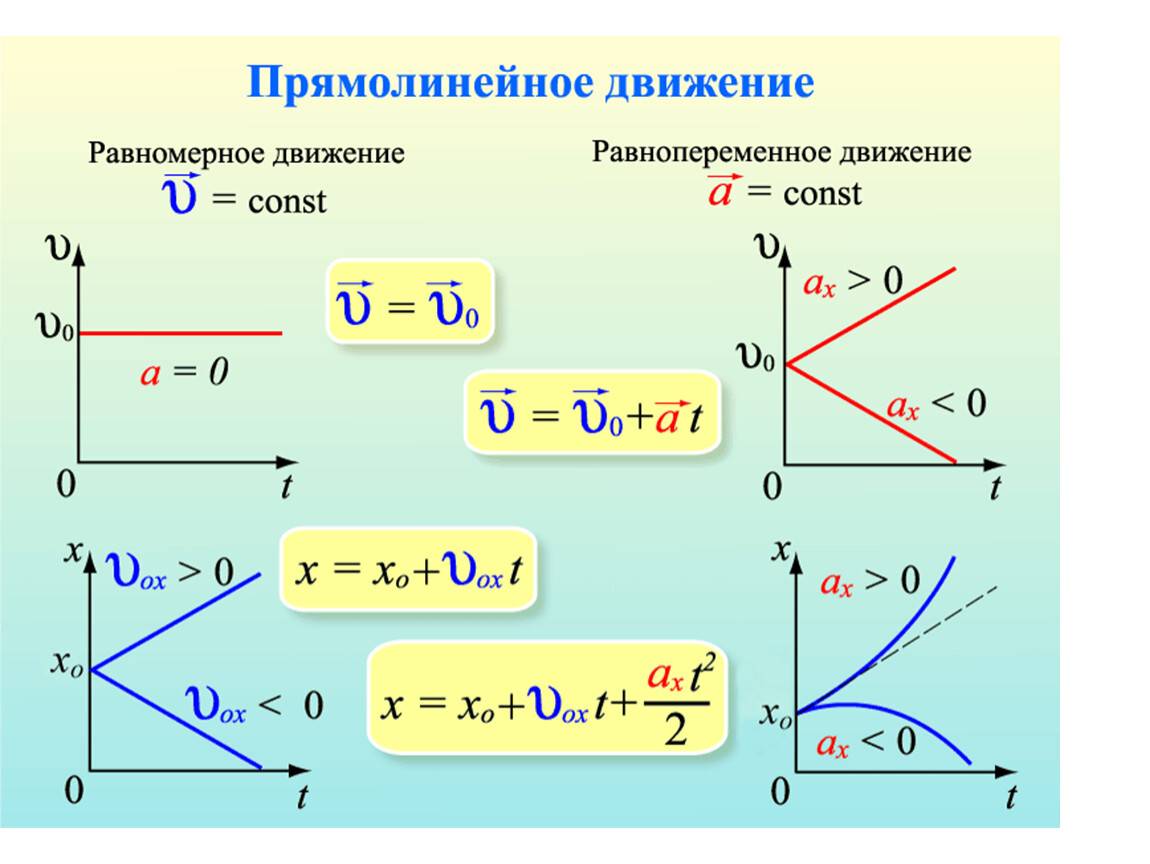
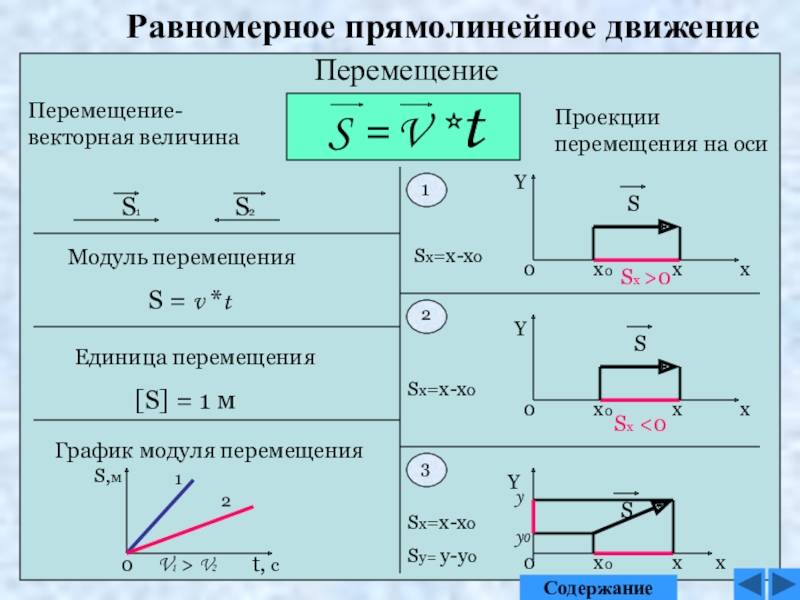
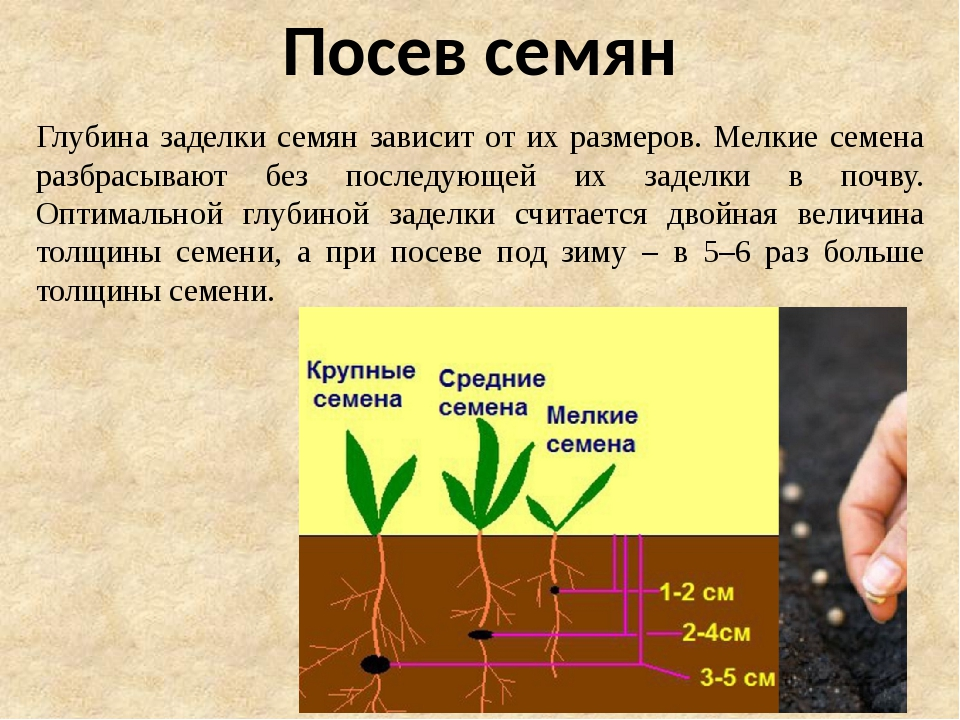
Равномерное движение: суть и примеры

Примеры равномерного движения можно наблюдать на практике. Например, автомобиль, движущийся по прямой дороге с постоянной скоростью, будет двигаться равномерно. Аналогичным образом, поезд, следующий по прямому пути с постоянной скоростью, также совершает равномерное движение.

Равномерное движение имеет простую математическую модель. Величина скорости определяется как отношение пройденного расстояния к затраченному времени. Если величина скорости остается постоянной, то и пройденное расстояние будет пропорционально времени. Таким образом, скорость tела в равномерном движении может быть рассчитана по формуле:

скорость = пройденное расстояние / время

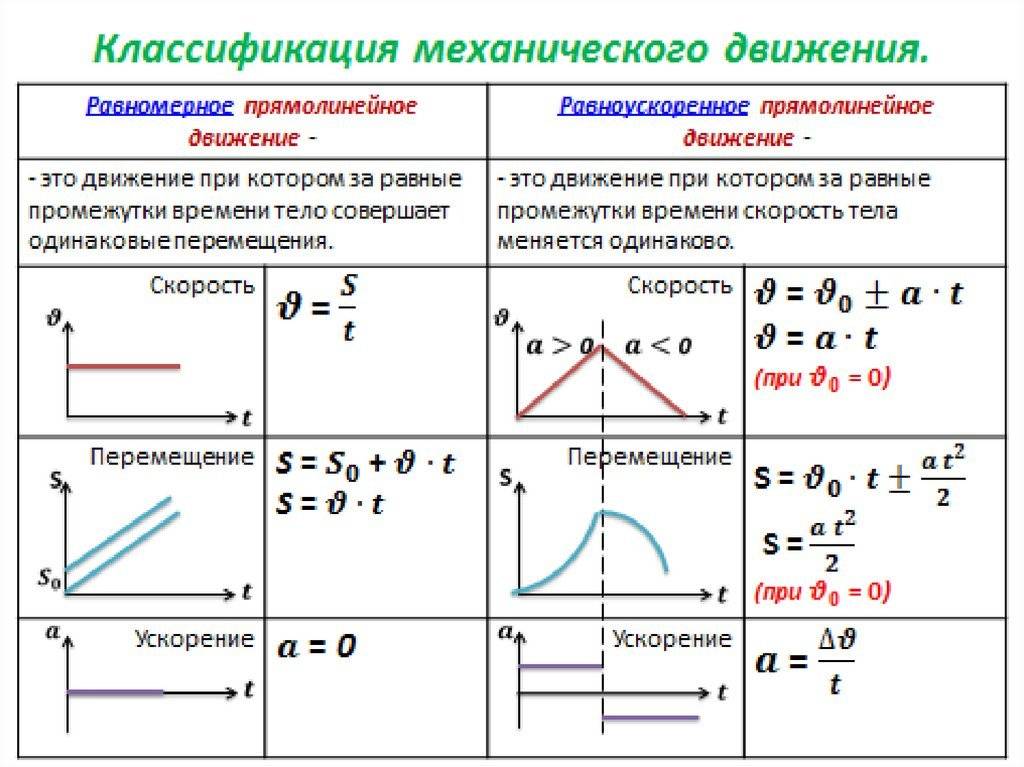
Равномерное движение

Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

График скорости (проекции скорости)

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью $ t $, тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью $ t $, тело движется против оси ОХ.

Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)

График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью $ t $, тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью $ t $, тело движется против оси ОХ.

По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время $ t $. Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: $ x=x(t) $.

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Примеры равноускоренного движения в физике

1. Свободное падение тела.

Свободное падение — это пример равноускоренного движения, когда тело свободно падает под воздействием гравитационной силы Земли. В данном случае ускорение равно ускорению свободного падения, примерно равному 9,8 м/с^2. Такое движение применяется, например, при изучении парашютного спорта или броска предметов с высоты.

2. Движение тела по наклонной плоскости.

Движение тела по наклонной плоскости является ещё одним примером равноускоренного движения. При движении тела по наклонной плоскости его скорость увеличивается равномерно со временем. Ускорение такого движения зависит от угла наклона плоскости и составляет компоненту силы тяжести, направленную вдоль плоскости. Примером такого движения может быть, например, скольжение саней по горке или спуск шарика по наклонной равномерно изогнутой дорожке.

3. Движение автомобиля с включенным круиз-контролем.

Когда автомобиль движется с включенным круиз-контролем, двигатель поддерживает постоянную скорость путем применения постоянного ускорения или замедления. Такое движение является примером равноускоренного движения. Круиз-контроль применяется, чтобы обеспечить комфортное движение на дороге при поездке на большие расстояния.

Приведённые примеры демонстрируют разнообразные ситуации, в которых можно наблюдать равноускоренное движение. Они позволяют лучше понять основные законы и принципы физики, связанные с равноускоренным движением.

Основные понятия и законы динамики

Часть механики, изучающая причины, вызвавшие ускорение тел, называется динамикой

Первый закон Ньютона:
Cуществуют такие системы отсчёта, относительно которых тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела или действие других тел скомпенсировано.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при уравновешенных внешних силах, действующих на него, называется инертностью. Явление сохранения скорости тела при уравновешенных внешних силах называют инерцией. Инерциальными системами отсчёта называют системы, в которых выполняется первый закон Ньютона.

Принцип относительности Галилея:во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково, т.е. подчиняются одинаковым законамМасса — это мера инертности телаСила — это количественная мера взаимодействия тел.

Второй закон Ньютона:Сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этой силой:
$F{→} = m⋅a{→}$

Сложение сил заключается в нахождении равнодействующей нескольких сил, которая производит такое же действие, как и несколько одновременно действующих сил.

Третий закон Ньютона: Силы, с которыми два тела действуют друг на друга, расположены на одной прямой, равны по модулю и противоположны по направлению:
$F_1{→} = -F_2{→} $

III закон Ньютона подчёркивает, что действие тел друг на друга носит характер взаимодействия. Если тело A действует на тело B, то и тело B действует на тело
A (см. рис.).
Или короче, сила действия равна силе противодействия. Часто возникает вопрос: почему лошадь тянет сани, если эти тела взаимодействуют с равными силами? Это возможно только за счёт взаимодействия с третьим телом — Землёй. Сила, с которой копыта упираются в землю, должна быть больше, чем сила трения саней о землю. Иначе копыта будут проскальзывать, и лошадь не сдвинется с места.
Если тело подвергнуть деформации, то возникают силы, препятствующие этой деформации. Такие силы называют силами упругости.

Закон Гука записывают в виде
где k — жёсткость пружины, x — деформация тела. Знак «−» указывает, что сила и деформация направлены в разные стороны.

При движении тел друг относительно друга возникают силы, препятствующие движению. Эти силы называются силами трения. Различают трение покоя и трение скольжения. Сила трения скольжения подсчитывается по формуле
где N — сила реакции опоры, µ — коэффициент трения.
Эта сила не зависит от площади трущихся тел. Коэффициент трения зависит от материала, из которого сделаны тела, и качества обработки их поверхности.

Трение покоя возникает, если тела не перемещаются друг относительно друга. Сила трения покоя может меняться от нуля до некоторого максимального значенияГравитационными силами называют силы, с которыми любые два тела притягиваются друг к другу.

Закон всемирного тяготения:Весом телаСила тяжестиНевесомостьюИскусственный спутник ЗемлиПервая космическая скорость

1.3. Основные понятия и законы статики и гидростатики

устойчивое, неустойчивое и безразличное.устойчивое равновесие.неустойчивое положениебезразличноеПлечом силыУсловие равновесия рычага:Давлениемзакон Паскаля:Гидравлический прессA1 = A2.силой Архимедазакон Архимеда_жидк_погрУсловие плавания тела

1.4. Законы сохранения

Импульсом телаимпульсом силы.закон сохранения импульсаМеханической работойМощностьэнергией.кинетическую и потенциальную.кинетической энергией.потенциальной энергией.Энергия сжатой пружины:механическую энергию.закон сохранения механической энергии

1.5. Механические колебания и волны

КолебаниямиГармоническими колебаниямиамплитудой колебанийПериодом TЧастотой периодических колебаний-1Математическим маятникомПериод колебаний математического маятникаПериод колебаний груза на пружинеРаспространение колебаний в упругих средах.поперечнойпродольнойДлиной волныЗвуковыми волнами

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Обозначение – $ g $, единицы измерения – м/с2.

Важно! $ g $ = 9,8 м/с2, но при решении задач считается, что $ g $ = 10 м/с2

Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

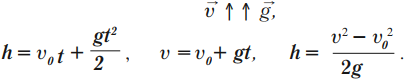
Если тело падает вниз без начальной скорости, то $ v_0 $ = 0.
Время падения рассчитывается по формуле:

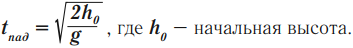
Тело брошено вверх:

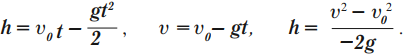
Если брошенное вверх тело достигло максимальной высоты, то $ v $ = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

равномерного движения по горизонтали со скоростью $ v_0=v_{0x} $;
равноускоренного движения по вертикали с ускорением свободного падения $ g $ и без начальной скорости $ v_{0y}=0 $.

Уравнение скорости:

Уравнение координаты:

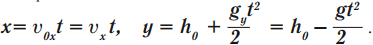
Скорость тела в любой момент времени:

Дальность полета:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

равномерного движения по горизонтали;
равноускоренного движения по вертикали с ускорением свободного падения.

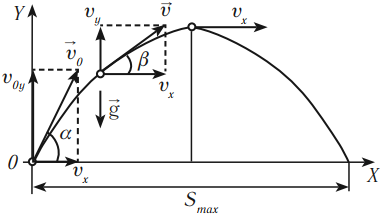
Уравнение скорости:

Уравнение координаты:

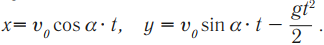
Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Время полета:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е

тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость $ v_0 $, с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол $ \alpha $, под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Кинематика — описание

Кинематика является разделом механики, цель которого — изучение механического движения тел с пренебрежением к причинам, вызывающим это движение.

Механика представляет собой научную область физики, которой посвящены исследования механического движения тел. Основной целью данного направления служит определение точного положения тела в пространстве в любой момент времени. Важным понятием этого раздела является материальная точка в виде тела с определенной массой и размерами, которыми можно пренебречь для решения задачи при наличии следующих условий:

Путь, который преодолевает тело, существенно больше, чем его размеры.
Расстояние между телами значительно превышает их размеры.
Объект совершает поступательное движение.

Движение тела рассматривают в системе отсчета, состоящей из системы координат и прибора, измеряющего время. Траекторией называют линию, которую объект описывает, совершая движение. Путь является скалярной величиной, определяемой как длина траектории. Перемещением обозначают вектор, который соединяет начальное и конечное положение тела, преодолеваемое им в течение определенного промежутка времени.

Совершая движение, тело может только увеличивать пройденный путь, при этом перемещение увеличивается или уменьшается. К примеру, уменьшение перемещения наблюдается во время обратного движения тела. Если объект движется прямолинейно в одном направлении, то путь определяется модулем перемещения. В случае криволинейного движения — путь превышает перемещение. При рассмотрении замкнутой траектории перемещение будет равно нулю.

Закон сложения скоростей.

Пусть имеются две системы отсчёта. Одна из них связана с неподвижным телом отсчёта . Эту систему отсчёта обозначим и будем называть неподвижной. Вторая система отсчёта, обозначаемая , связана с телом отсчёта , которое движется относительно тела со скоростью . Эту систему отсчёта называем движущейся. Дополнительно предполагаем, что координатные оси системы перемещаются параллельно самим себе (нет вращения системы координат), так что вектор можно считать скоростью движущейся системы относительно неподвижной.

Неподвижная система отсчёта обычно связана с землёй. Если поезд плавно едет по рельсам со скоростью , это система отсчёта, связанная с вагоном поезда, будет движущейся системой отсчёта .

Заметим, что скорость любой точки вагона (кроме вращающихся колёс!) равна . Если муха неподвижно сидит в некоторой точке вагона, то относительно земли муха движется со скоростью . Муха переносится вагоном, и потому скорость движущейся системы относительно неподвижной называется переносной скоростью.

Предположим теперь, что муха поползла по вагону. Скорость мухи относительно вагона (то есть в движущейся системе ) обозначается и называется относительной скоростью. Скорость мухи относительно земли (то есть в неподвижной системе ) обозначается и называется абсолютной скоростью.

Выясним, как связаны друг с другом эти три скорости – абсолютная, относительная и переносная. На рис. 4 муха обозначена точкой .Далее: – радиус-вектор точки в неподвижной системе ; – радиус-вектор точки в движущейся системе ; – радиус-вектор тела отсчёта в неподвижной системе .

Рисунок 4.

Как видно из рисунка,

Дифференцируя это равенство, получим:

(производная суммы равна сумме производных не только для случая скалярных функций, но и для векторов тоже). Производная есть скорость точки в системе , то есть абсолютная скорость:

Аналогично, производная есть скорость точки в системе , то есть относительная скорость:

А что такое ? Это скорость точки в неподвижной системе, то есть – переносная скорость движущейся системы относительно неподвижной:

В результате из (3) получаем:

Закон сложения скоростей. Скорость точки относительно неподвижной системы отсчёта равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы. Иными словами, абсолютная скорость есть сумма переносной и относительной скоростей.

Таким образом, если муха ползёт по движущемуся вагону, то скорость мухи относительно земли равна векторной сумме скорости вагона и скорости мухи относительно вагона. Интуитивно очевидный результат!

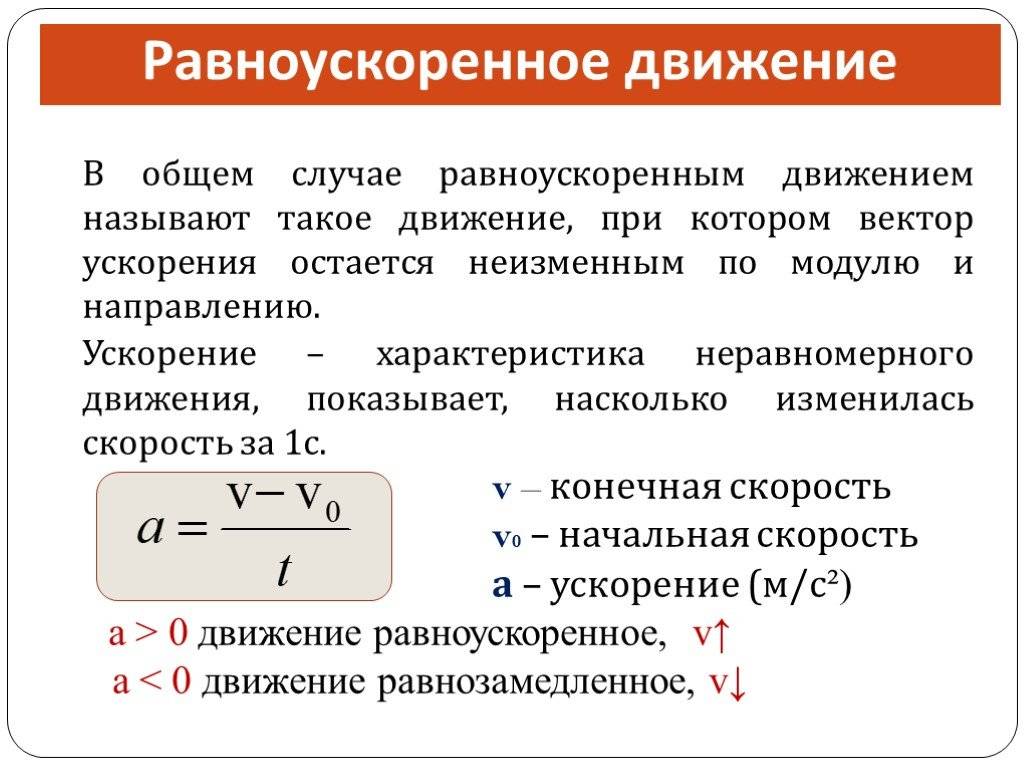
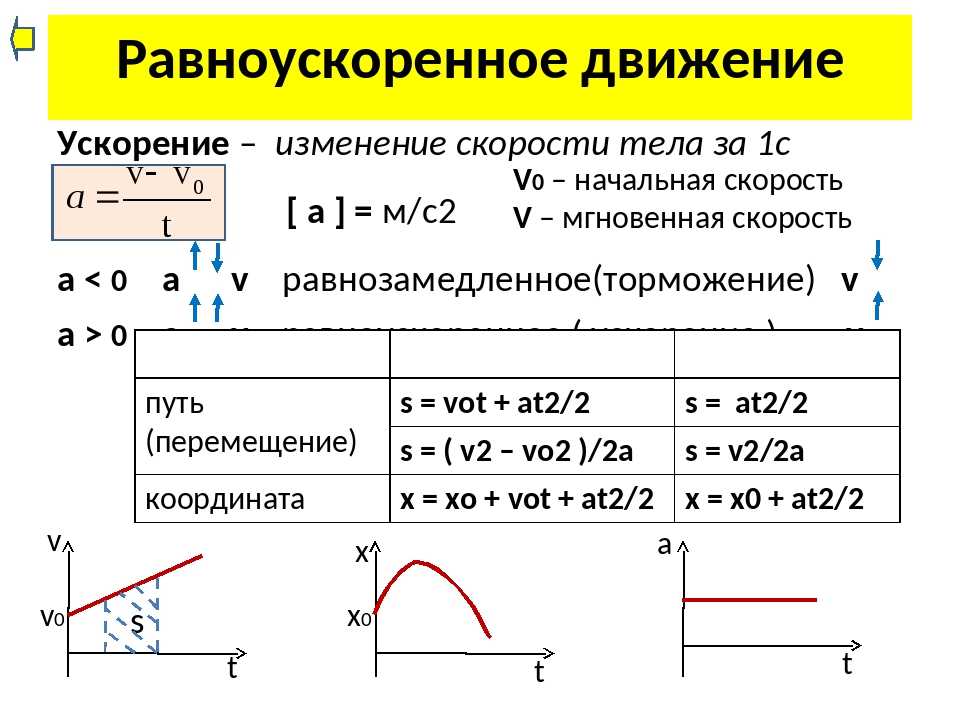
Равноускоренное движение

Равноускоренное движение не обладает одинаковой скоростью на протяжении всего пути прохождения. в таком случае присутствует ускорение, которое отвечает за постоянное увеличение скорости. Ускорение в таком виде движения остается неизменным, а скорость постоянно и равномерно растет. Теоретически до бесконечности , если объект движется относительно другого объекта, до скорость меньшей скорости света, если его скорость считается относительного самого объекта.

Равноускоренное движение

Если в расчеты включаются другие свойства, то конечная скорость будет еще ниже. Помимо равноускоренного существует так же равнозамедленное движение, где модуль скорость равномерно снижается. Так же равноускоренное движение может протекать в нескольких измерениях, в связи с чем оно бывает:

Одномерным.
Многомерным.

В случае первого — движение осуществляется вдоль одной оси координат. В случае второго могут быть добавлены и другие измерения.

Задачи по кинематике, их решение

Задача 1

Рассмотрим путь велосипедиста из одного населенного пункта в другой. Половина расстояния была преодолена со скоростью 12 км/ч ($v_1$). Далее половину оставшегося времени он ехал со скоростью 6 км/ч ($v_2$). Остаток расстояния путник преодолел пешком со скоростью 4км/ч ($v_3$). Необходимо рассчитать среднюю скорость на всем пути следования велосипедиста.

Решение

Данный пример относится к теме равномерного прямолинейного движения одного тела. Процесс можно изобразить схематично:

$S = S_1 + S_2 + S_3$

$t = t_1 + t_2 + t_3$

На каждый отрезок пути необходимо составить уравнение движения:

$S_1 = v_1t_1$

$S_2 = v_2t_2$

$S_3 = v_3t_3$

Далее можно представить дополнительные условия задачи:

$S_1 = S_2 + S_3$

$t_2 = t_3$

$v_{sr}=\frac{S}{t}=\frac{S_{1}+S_{2}+S_{3}}{t_{1}+t_{2}+t_{3}}$

Следует преобразить формулу и подставить числовые значения:

$v_{sr}=\frac{2S_{1}}{\frac{S_{1}}{v_{1}}+\frac{2S_{1}}{v_{2}+v_{3}}}=\frac{2v_{1}\left(v_{2}+v_{3} \right)}{2v_{1}+v_{2}+v_{3}}$

$v_{sr}=\frac{2\times 12\left(6+4 \right)}{2\times 12+6+4}=7$

Ответ: средняя скорость составляет $7$ км/ч.

Задача 2

Тело подбросили вертикально вверх. Начальная скорость при этом составила 3,13 м/с ($v_0$). В момент, когда данное тело достигло максимальную высоту полета, из начального пункта подбросили второе тело с такой же начальной скоростью, как у первого. Необходимо определить на каком расстоянии от точки бросания встретятся тела. Сопротивлением воздуха при решении можно не учитывать.

Решение

Схематично перемещение тел можно представить следующим образом:

Формула, описывающая движение тела, которое подбросили вверх, необходима для вычисления координаты движущегося тела в любое время. Для первого тела справедливо уравнение:

$h=v_{0}t_{1}-\frac{gt_{1}^{2}}{2}$

Для второго тела можно представить следующую формулу:

$h=v_{0}t_{2}-\frac{gt_{2}^{2}}{2}$

Следующую формулу можно составить на основании условия задачи, в котором указано, что второе тело бросили позднее первого на время максимального подъема:

$t_{1}-t_{2}=\frac{v_{0}}{g}$

Объединяя уравнения в систему из трех формул относительно величины $h$ получим:

$h=\frac{3}{4}\frac{v_{0}^{2}}{2g}$

$h=\frac{3}{4}\frac{3.13^{2}}{2*9.8}=0.37$

Ответ: тела встретятся на высоте $0,37$ м.

Задача 3

Камень, находясь в свободном падении, вторую часть пути преодолел за 1 секунду. Необходимо вычислить высоту $h$, с которой упал камень.

Решение

Ось Y системы координат, в которых падает камень, направлена вертикально вниз. В качестве начала координат можно принять точку, из которой камень упал. Закон перемещения данного тела в проекции на ось будет обладать следующим видом:

$h=v_{0}t+\frac{gt^{2}}{2}$

$h=\frac{gt^{2}}{2}$

$v=v_{0}t+gt$

$v=gt$

Время падения камня рассчитывается по формуле:

$t=\sqrt{\frac{2h}{g}}$

Для середины пути, который преодолел камень, справедливы уравнения:

$\frac{h}{2}=\frac{gt_{1}^{2}}{2}$

$t_{1}=\sqrt{\frac{h}{g}}$

Время $t_2$, которое потребовалось телу на преодоление второй половины пути, указанное в условии задачи, рассчитывается по формуле:

$t_{2}=t-t_{1}=\sqrt{\frac{2h}{g}}-\sqrt{\frac{h}{g}}$

$t_{2}^{2}=\frac{h}{g}\left(\sqrt{2} -1\right)^{2}$

Исходя из данного уравнения, можно вычислить высоту:

$t_{2}^{2}=\frac{h}{g}\left(\sqrt{2} -1\right)^{2}$

$h=\frac{t_{2}^{2}g}{\left(\sqrt{2}-1 \right)^{2}}=\frac{9,81}{0,17}=57,7$

Ответ: камень упал с высоты $57,7$ м.

Разница в изменении траектории движения

Одно из принципиальных отличий между равноускоренным движением и равномерным движением заключается в изменении траектории движения.

В равномерном движении траектория остается прямолинейной и параллельной оси, по которой движется тело. Скорость движения при этом остается постоянной. Например, если автомобиль движется по прямой дороге с постоянной скоростью, то его траектория будет являться прямой линией.

В случае равноускоренного движения траектория изменяется. Это происходит из-за воздействия ускорения на тело. Ускорение изменяет скорость движения тела, что влечет за собой изменение его положения с течением времени. Траектория равноускоренного движения может быть разнообразной и зависит от направления и величины ускорения. Например, если тело движется по окружности радиусом R с угловым ускорением α, то его траектория будет являться окружностью.

Таким образом, равномерное и равноускоренное движения различаются по изменению траектории: в равномерном движении траектория остается прямолинейной и параллельной оси, а в равноускоренном движении траектория может быть разнообразной, в зависимости от величины и направления ускорения.

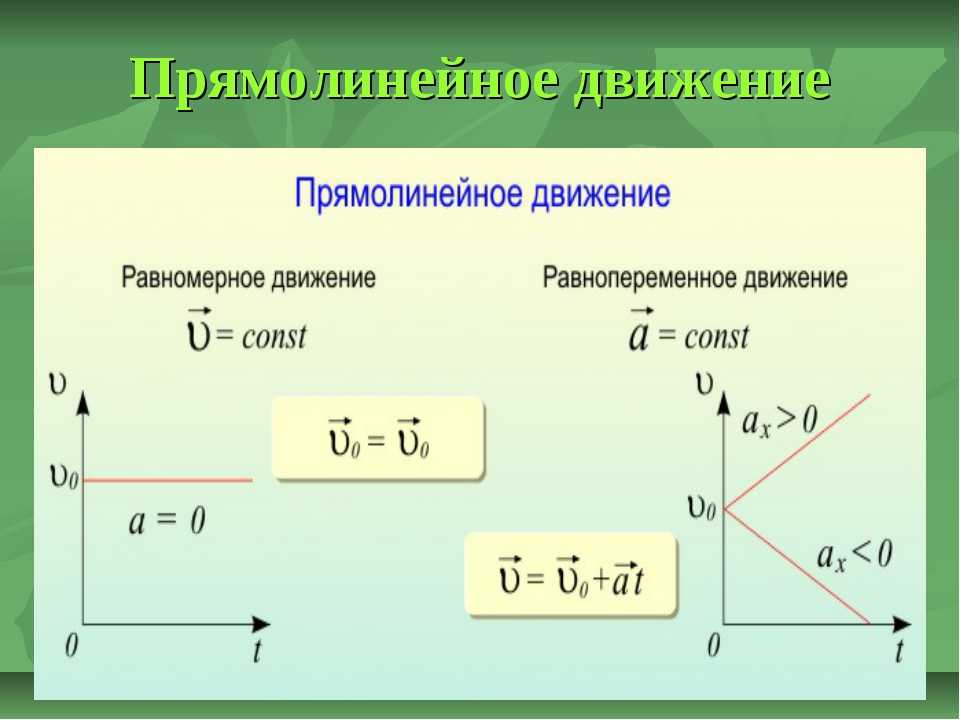
Прямолинейное равноускоренное движение

Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.

Итак, равноускоренное прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.

Уравнение движения и формула конечной скорости

Основная задача механики не поменялась по ходу текста — определение положения тела относительно других тел в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.

Уравнение движения для равноускоренного движения

x(t) — искомая координата в момент времени t x — начальная координата v_0x — начальная скорость тела в [м/с] t — время a_x — ускорение [м/с 2 ]

Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:. Формула конечной скорости

Формула конечной скорости

— конечная скорость тела [м/с] — начальная скорость тела [м/с] — время — ускорение [м/с 2 ]

Задача

Найдите местоположение автобуса, который разогнался до скорости 60 км/ч за 3 минуты, через 0,5 часа после начала движения из начала координат.

Решение:

Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:

Так как автобус двигался с места, . Значит

Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.

3 минуты = 3/60 часа = 1/20 часа = 0,05 часа

Подставим значения: a = v/t = 60/0,05 = 1200 км/ч 2 Теперь возьмем уравнение движения. x(t) = x + v_0xt + a_xt 2 /2

Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:

Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.

Подставим циферки: км

Ответ: через полчаса координата автобуса будет равна 150 км.

Сравнение двух типов движения

Прямолинейное равномерное движение:

Преимущество прямолинейного равномерного движения заключается в своей простоте и прогнозируемости. Все объекты, движущиеся с постоянной скоростью, будут двигаться по прямой линии без изменения скорости.
Этот тип движения легко описывается с помощью уравнений и формул. Получение точных результатов и прогнозирование позиции и скорости объекта в будущем является относительно простым.
Прямолинейное равномерное движение применимо к многим реальным ситуациям, таким как движение автомобилей по прямым дорогам или движение спутников вокруг Земли.

Равноускоренное движение:

Сильная сторона равноускоренного движения заключается в его способности изменять скорость объекта со временем. Это позволяет описывать сложные и динамичные физические явления, такие как падение тела или движение автомобиля с ускорением.
Уравнения равноускоренного движения позволяют прогнозировать будущую позицию и скорость объекта с учетом ускорения. Это делает его основным инструментом для анализа и моделирования многих физических процессов.
Равноускоренное движение играет важную роль в механике и других областях науки. Оно позволяет понять и описать такие явления, как движение тел при силе тяжести или движение частиц в электромагнитных полях.

Несмотря на то, что прямолинейное равномерное движение и равноускоренное движение имеют свои собственные преимущества и применения, они являются упрощенными моделями и не всегда полностью соответствуют реальным физическим процессам. Для более точных анализов и описаний часто требуется использование более сложных моделей и уравнений.

Движение по вертикали

Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с 2 , а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).

Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с 2 . В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с 2 .

Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с 2 .

Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.

Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.

Темы кодификатора ЕГЭ: механическое движение и его виды, относительность механического движения, скорость, ускорение.

Понятие движения является чрезвычайно общим и охватывает самый широкий круг явлений. В физике изучают различные виды движения. Простейшим из них является механическое движение. Оно изучается в механике. Механическое движение — это изменение положение тела (или его частей) в пространстве относительно других тел с течением времени.

Если тело A меняет своё положение относительно тела B, то и тело B меняет своё положение относительно тела A. Иначе говоря, если тело A движется относительно тела B, то и тело B движется относительно тела A. Механическое движение является относительным — для описания движения необходимо указать, относительно какого тела оно рассматривается.

Так, например, можно говорить о движении поезда относительно земли, пассажира относительно поезда, мухи относительно пассажира и т. д. Понятия абсолютного движения и абсолютного покоя не имеют смысла: пассажир, покоящийся относительно поезда, будет двигаться с ним относительно столба на дороге, совершать вместе с Землёй суточное вращение и двигаться вокруг Солнца. Тело, относительно которого рассматривается движение, называется телом отсчёта.

Основной задачей механики является определение положения движущегося тела в любой момент времени. Для решения этой задачи удобно представить движение тела как изменение координат его точек с течением времени. Чтобы измерить координаты, нужна система координат. Чтобы измерять время, нужны часы. Всё это вместе образует систему отсчёта.

Рисунок 1.

Вектор называется радиус-вектором точки . Координаты точки являются в то же время координатами её радиус-вектора . Решение основной задачи механики для точки состоит в нахождении её координат как функций времени: . В ряде случаев можно отвлечься от формы и размеров изучаемого объекта и рассматривать его просто как движущуюся точку.

Материальная точка — это тело, размерами которого можно пренебречь в условиях данной задачи. Так, поезд можно считать материальной точкой при его движении из Москвы в Саратов, но не при посадке в него пассажиров. Землю можно считать материальной точкой при описании её движения вокруг Солнца, но не её суточного вращения вокруг собственной оси.

К характеристикам механического движения относятся траектория, путь, перемещение, скoрость и ускорение.

Особенности равноускоренного движения

Одной из особенностей равноускоренного движения является то, что скорость объекта нарастает и изменяется с постоянной скоростью. Это означает, что каждую секунду объект приобретает одинаковую величину скорости.

Для объяснения равноускоренного движения можно использовать следующий пример. Представим, что автомобиль едет по прямой дороге с установленным круиз-контролем. Круиз-контроль позволяет поддерживать постоянную скорость, что является примером равномерного движения. Однако, если водитель решит увеличить скорость автомобиля с постоянным ускорением, то это будет примером равноускоренного движения.

В равноускоренном движении можно выделить несколько особенностей:

Ускорение является постоянным и неизменным во время движения.
Скорость объекта нарастает с течением времени.
Пройденное расстояние каждую секунду увеличивается в геометрической прогрессии.
Объект движется все быстрее и быстрее с каждой секундой.

Равноускоренное движение находит свое применение в разных сферах. Например, при описании движения падающих тел или движения некоторых видов механизмов.

Что такое скорость?

На интуитивном уровне это понятно. Но давайте попробуем вникнуть поглубже. В чем всегда измеряется скорость? В автомобиле это обычно километры в час (км/ч), измеряется при помощи спидометра. То есть спидометр машины показывает, сколько километров проедет машина за один час, если не будет менять скорость. Точно так же скорость можно измерять в метрах в секунду (м/с), километрах в секунду (км/с) и т.д. Значит, если я умножу скорость на количество часов, которые едет машина с этой скоростью, то получу расстояние, пройденное машиной за это время. Можно записать в виде известной формулы движения с постоянной скоростью:

Итак, при движении с постоянной скоростью $V$, можно посчитать расстояние $S$, которое проходит тело за время $t$.

Теперь давайте предположим, что машина двигается с постоянной скоростью 1 (м/с) влево из начальной точки с координатой $x_0=3(м)$. Это означает, что машина за 1 секунду сдвинется на $S=V*t=1*1=1(м)$ метр влево, то есть окажется в точке с координатой $2$ (м). Через 2 секунды она пройдет расстояние $S=V*t=1*2=2(м)$ и попадет в координату $1$(м), а через 6 секунд на $S=V*t=1*6=6(м)$ и окажется в координате $-3$(м).

Скорость кроме величины еще имеет направление – в нашем случае это означает, что если машина едет вправо (туда же, куда направлена ось $х$), то скорость будет положительна, а если влево (в противоположную сторону направлению оси $х$), то скорость будет отрицательна.

Все, что имеет величину и направление, называется вектором. То есть скорость ни что иное, как вектор. Вектор – это ключевое понятие физики. Мы часто будем сталкиваться с величинами, у которых кроме числа есть еще и направление – ускорение, сила.

Немного отвлечемся, и обсудим, что такое вектор.

Основные понятия и законы кинематики

кинематикойМеханическим движениемСистемой отсчётаТелом отсчётаМатериальной точкойТраекториейпрямолинейноекриволинейное
Путь — это длина траектории, которую описывает материальная точка за данный промежуток времени. Это скалярная величина.Перемещение — это вектор, соединяющий начальное положение материальной точки с её конечным положением (см. рис.).

Очень важно понимать, чем путь отличается от перемещения. Самое главной отличие в том, что перемещение – это вектор с началом в точке отправления и с концом в точке назначения (при этом абсолютно неважно, каким маршрутом это перемещение совершалось)

А путь – это, наборот, скалярная величина, отражающая длину пройденной траектории.

Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещенияСкоростью равномерного прямолинейного движения называют отношение перемещения ко времени, за которое это перемещение произошло:

Для неравномерного движения пользуются понятием средней скорости. Часто вводят среднюю скорость как скалярную величину. Это скорость такого равномерного движения, при котором тело проходит тот же путь за то же время, что и при неравномерном движении:

Мгновенной скоростью называют скорость тела в данной точке траектории или в данный момент времени.Равноускоренное прямолинейное движение — это прямолинейное движение, при котором мгновенная скорость за любые равные промежутки времени изменяется на одну и ту же величину

Ускорением

Зависимость координаты тела от времени в равномерном прямолинейном движении имеет вид: x = x + V_xt, где x — начальная координата тела, V_x — скорость движения.Свободным падением называют равноускоренное движение с постоянным ускорением g = 9,8 м/с2, не зависящим от массы падающего тела. Оно происходит только под действием силы тяжести.

Скорость при свободном падении рассчитывается по формуле:
Перемещение по вертикали рассчитывается по формуле:

Одним из видов движения материальной точки является движение по окружности. При таком движении скорость тела направлена по касательной, проведённой к окружности в той точке, где находится тело (линейная скорость). Описывать положение тела на окружности можно с помощью радиуса, проведённого из центра окружности к телу. Перемещение тела при движении по окружности описывается поворотом радиуса окружности, соединяющего центр окружности с телом. Отношение угла поворота радиуса к промежутку времени, в течение которого этот поворот произошёл, характеризует быстроту перемещения тела по окружности и носит название угловой скорости
ω:
Угловая скорость связана с линейной скоростью соотношением где r — радиус окружности.
Время, за которое тело описывает полный оборот, называется периодом обращения. Величина, обратная периоду — частота обращения — ν
Поскольку при равномерном движении по окружности модуль скорости не меняется, но меняется направление скорости, при таком движении существует ускорение. Его называют центростремительным ускорением, оно направлено по радиусу к центру окружности: