В чем разница между натуральными и целыми числами?

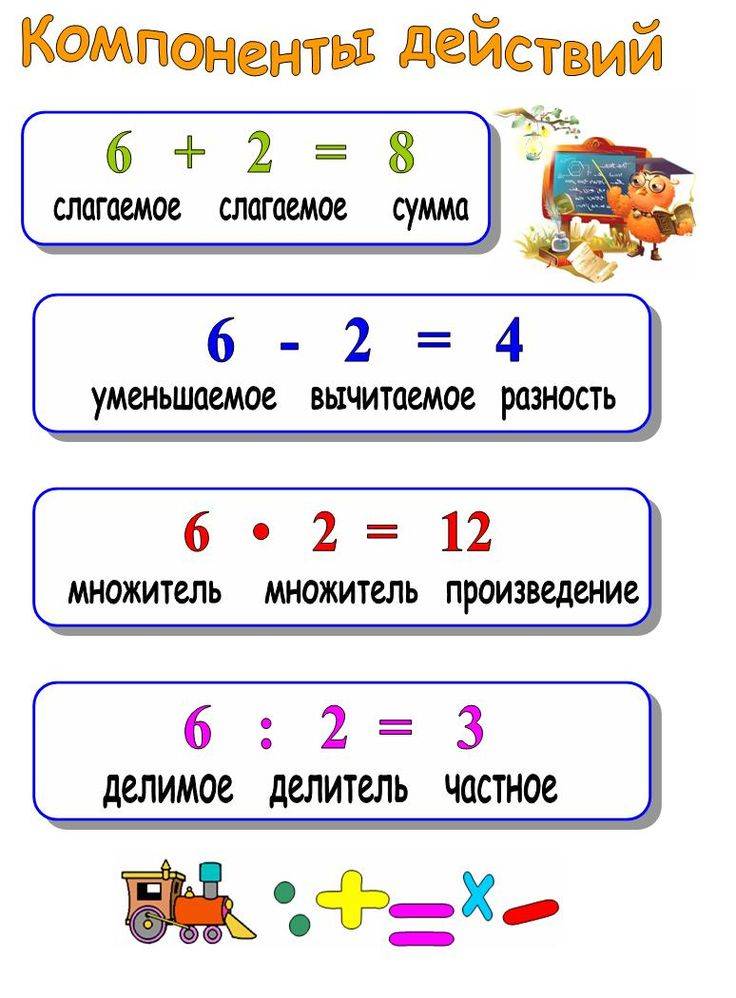
Операции с целыми числами

Основные операции с целыми числами включают:

1. Сложение: Сложение целых чисел выполняется по правилам сложения натуральных чисел. Если оба числа положительные, то их сумма будет также положительным числом. Если оба числа отрицательные, то сумма будет также отрицательным числом. Если одно число положительное, а другое отрицательное, то сумма будет равна разности абсолютных значений чисел, а знак суммы будет тем же, что и у числа с большим абсолютным значением. Например, -5 + 3 = -2.

2. Вычитание: Вычитание целых чисел также выполняется по правилам вычитания натуральных чисел. Если мы вычитаем положительное число из положительного числа, получим положительную разность. Если мы вычитаем отрицательное число из отрицательного числа, получим положительную разность. Если мы вычитаем положительное число из отрицательного числа, получим отрицательную разность. Если мы вычитаем отрицательное число из положительного числа, получим положительную сумму. Например, 7 — (-2) = 9.

3. Умножение: Умножение целых чисел выполняется по правилам умножения натуральных чисел. Если оба числа положительные или оба числа отрицательные, то их произведение будет положительным числом. Если одно число положительное, а другое отрицательное, то произведение будет отрицательным числом. Например, 3 * (-4) = -12.

4. Деление: Деление целых чисел также выполняется по правилам деления натуральных чисел. Частное от деления двух целых чисел может быть положительным или отрицательным. Остаток от деления также может быть положительным или отрицательным. Например, 14 / 3 = 4 (остаток 2), а (-14) / 3 = -5 (остаток -1).

Понятие

Данное понятие появилось в математике одним из первых. В древности люди перечисляли предметы на пальцах, и им вполне этого хватало. Но с бурным развитием торговли и ростом количества продукции на рынках одних пальцев для счета стало не хватать. Поэтому древние люди придумали символы, обозначающие количество чего-либо, которые они использовали для перечисления скота, различных вещей и т.д. Чуть позже числа вошли в науку математику, где стали активно применяться в качестве материала для многочисленных алгебраических преобразований.Натуральные числа – все символы, используемые при счете каких-либо предметов, тем самым вычисляя их последовательность и количество. Все отрицательные и дробные числа не являются натуральными.
Соответственно – наименьшей является единица. Наибольшего натурального числа не существует, так как счет можно продолжать до бесконечности.
Рис. 1. Определение натуральных чиселВернемся в древние времена. Тогда числа записывали чаще с помощью палочек или любых других примитивных знаков:

• 1 = I;
• 2 = II;
• 3 = III.

Но когда палочек приходилось писать слишком много (100, 1000), люди задумались над более емкой системой записи количества предметов. Так, арабы придумали и завезли в Европу свои цифры, которые на континенте назвали арабскими. Мы прекрасно знаем все эти цифры:

0 1 2 3 4 5 6 7 8 9 (10 штук).

Из данных цифр можно составить абсолютно все натуральные числа. Их множество обозначается знаком N.

Как выбрать подходящий тип чисел для конкретных задач

При работе с числами очень важно выбрать подходящий тип данных, который позволит эффективно выполнить конкретную задачу. Определение типа чисел зависит от ряда факторов, например, диапазона значений, требуемой точности и операций, которые нужно выполнить

Если вам нужно представить только целые положительные числа, можно использовать беззнаковые целочисленные типы данных, такие как , , и т.д. Они позволяют экономно использовать память и могут представить числа в определенном диапазоне. Если вам требуются отрицательные числа, вы можете использовать соответствующие типы данных с знаком, такие как , , и т.д.

Если вашей задачей является работа с вещественными числами, то вам потребуются типы данных, которые поддерживают дробные значения. В языках программирования обычно предоставляются типы данных для чисел с плавающей запятой, такие как и . Они позволяют хранить числа с большей точностью и имеют больший диапазон значений.

Если вам нужно работать с очень большими числами или числами с высокой точностью, вы можете использовать специальные библиотеки или типы данных, такие как или . Эти типы данных предоставляют возможность работы с произвольным количеством цифр и обеспечивают высокую точность результатов.

В итоге, выбор подходящего типа чисел зависит от ваших конкретных потребностей и требований задачи. Правильное использование типов данных поможет сделать программу эффективнее и избежать проблем с памятью, точностью или производительностью.

Виды чисел

• Натуральные – все положительные числа, которые мы используем для счета (2, 19, 56, 478, 2048 и т.д.). Ноль не является натуральным числом.
• Простые – натуральные числа, которые без остатка делятся только на единицу и само себя: 2, 3, 5, 7, 11 и т.д.
• Составные – числа, которые имеют три и более делителя.
• Целые – это положительные (больше нуля) и отрицательные (меньше нуля) числа, которые не имеют дробной части.
• Четные – целые числа, которые без остатка делятся на два: 2, 4, 6, 8, 10, 12 и т.д.
• Нечетные – целые числа, которые не делятся без остатка на два: 15, 21, 37, 41 и т.д.
• Вещественные – рациональные и иррациональные числа.
• Рациональные  – числа, которые можно представить в виде обыкновенной дроби.
• Иррациональные – бесконечные непериодические десятичные дроби, которые нельзя представить в виде обыкновенных.

Это числа, которые используются при счете: 1, 2, 3… и т.д.

Натуральные числа принято обозначать символом N.

Целые числа. Положительные и отрицательные числа

Два числа отличающиеся друг от друга только знаком, называются противоположными, например, +1 и -1, +5 и -5. Знак «+» обычно не пишут, но предполагают, что перед числом стоит «+». Такие числа называются положительными. Числа, перед которыми стоит знак «-«, называются отрицательными.

Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.

Рациональные числа

Это конечные дроби и бесконечные периодические дроби.

Множество рациональных чисел обозначается Q. Все целые числа являются рациональными.

Действительные числа

Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.

Комплексные числа

Комплексные числа– числа, являющиеся расширением множества действительных чисел. Они могут быть записаны в виде  z = x + iy, где i — т. н. мнимая единица, для которой выполняется равенство i2 = -1. Комплексные числа используются при решении задач электротехники, гидродинамики, картографии, квантовой механики, теории колебаний, теории хаоса, теории упругости и многих других. Комплексные числа подразделяются на алгебраические и трансцендентные.

При этом каждое действительное трансцендентное является иррациональным, а каждое рациональное число — действительным алгебраическим. Более общими (но всё ещё счётными) классами чисел, чем алгебраические, являются периоды, вычислимые и арифметические числа (где каждый последующий класс шире, чем предыдущий).

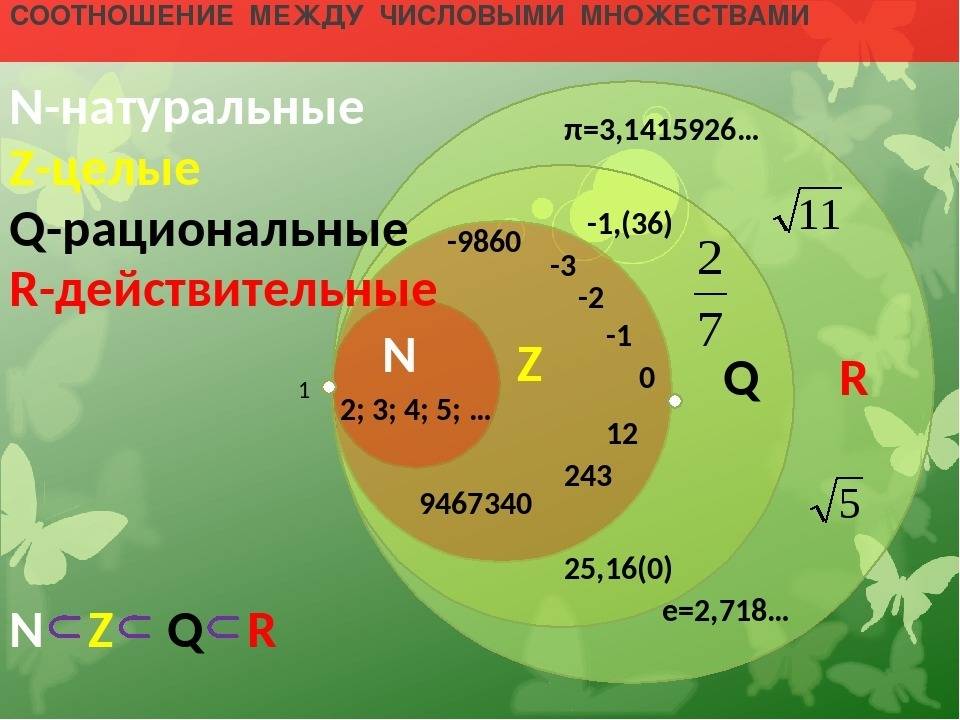
Т. е. множество натуральных чисел входит во множество целых чисел. Множество целых чисел входит во множество рациональных чисел. Множество рациональных чисел входит во множество действительных чисел. А множество действительных чисел входит во множество комплексных чисел.

Это высказывание можно проиллюстрировать с помощью кругов Эйлера: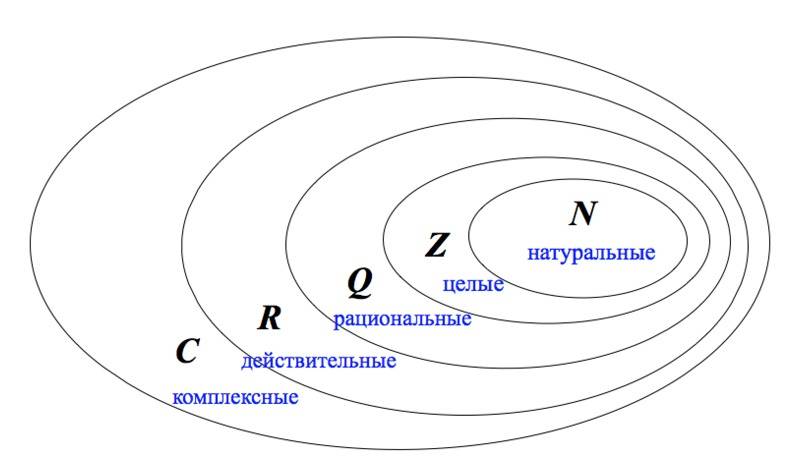

Числа: натуральные, целые, рациональные, иррациональные, действительные

Натуральные числа определение – это целые положительные числа. Натуральные числа используют для счета предметов и многих иных целей. Вот эти числа:

Это натуральный ряд чисел. Ноль натуральное число? Нет, ноль не является натуральным числом. Сколько натуральных чисел существует? Существует бесконечное множество натуральных чисел. Каково наименьшее натуральное число? Единица — это наименьшее натуральное число. Каково наибольшее натуральное число? Его невозможно указать, ведь существует бесконечное множество натуральных чисел.

Сумма натуральных чисел есть натуральное число. Итак, сложение натуральных чисел a и b:

с — это всегда натуральное число.

Произведение натуральных чисел есть натуральное число. Итак, произведение натуральных чисел a и b:

с — это всегда натуральное число.

Разность натуральных чисел Не всегда есть натуральное число. Если уменьшаемое больше вычитаемого, то разность натуральных чисел есть натуральное число, иначе — нет.

Частное натуральных чисел Не всегда есть натуральное число. Если для натуральных чисел a и b

где с — натуральное число, то это значит, что a делится на b нацело. В этом примере a — делимое, b — делитель, c — частное.

Делитель натурального числа — это натуральное число, на которое первое число делится нацело.

Каждое натуральное число делится на единицу и на себя.

Простые натуральные числа делятся только на единицу и на себя. Здесь имеется ввиду делятся нацело. Пример, числа 2; 3; 5; 7 делятся только на единицу и на себя. Это простые натуральные числа.

Единицу не считают простым числом.

Числа, которые больше единицы и которые не являются простыми, называют составными. Примеры составных чисел:

Единицу не считают составным числом.

Множество натуральных чисел составляют единица, простые числа и составные числа.

Множество натуральных чисел обозначается латинской буквой N.

Свойства сложения и умножения натуральных чисел:

переместительное свойство сложения

сочетательное свойство сложения

переместительное свойство умножения

сочетательное свойство умножения

распределительное свойство умножения

Целые числа

Целые числа — это натуральные числа, ноль и числа, противоположные натуральным.

Числа, противоположные натуральным — это целые отрицательные числа, например:

Множество целых чисел обозначается латинской буквой Z.

Рациональные числа

Рациональные числа — это целые числа и дроби.

Любое рациональное число может быть представлено в виде периодической дроби. Примеры:

Из примеров видно, что любое целое число есть периодическая дробь с периодом ноль.

Любое рациональное число может быть представлено в виде дроби m/n, где m целое число,n натуральное число. Представим в виде такой дроби число 3,(6) из предыдущего примера:

Другой пример: рациональное число 9 может быть представлено в виде простой дроби как 18/2 или как 36/4.

Ещё пример: рациональное число -9 может быть представлено в виде простой дроби как -18/2 или как -72/8.

Множество рациональных чисел обозначается латинской буквой Q.

Подробнее о рациональных числах в разделе Рациональные числа.

Числа: натуральные, целые, рациональные

Число – ядро счёта. Необходимость посчитать появилась ещё у первобытного человека. Для этого использовались свои способы и метки. Ребёнок умеет считать до того, как пойдёт в школу. Он может посчитать свои игрушки, пальчики на руках и другие объекты.

Числа, которые использует человек для счёта чего-либо, называются натуральными. Подсчитаем количество книг в библиотеке (одна книга, две книги, три книги). Натуральный ряд идёт с 1 (единицы) и выглядит так: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …и т. д. Нуль не входит в этот строй, поэтому не является натуральным. Мы не можем сосчитать то, чего нет.

• самое маленькое число в линии – это 1;
• наибольшего – отсутствует, считать можно до бесконечности;
• каждое следующее число увеличивается на 1.

Буквой N отмечается множество данных чисел.

Данные числа можно:

• складывать, 2+3=5;
• умножать, 3*10=30;
• вычитать, 35-5=20;
• делить, 45:9=5;
• возводить в степень, 3² (три в квадрате).

Цифра – это письменный знак для записи числа. Их всего десять – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Используя цифры 3, 5, 7, можно записать как 753.

Кажется, что в быту мы пользуемся только натуральным рядом, но это не так. В большей степени используются целые числа. С их участием можно посчитать, как в положительную, так и в отрицательную стороны. Натуральные входят в состав обширного множества целых. Всякое натуральное число — является целым. Они имеют пару в виде отрицательного (2 и -2, 70 и -70, 125 и -125). Со знаком минус — это целое отрицательное число.

Итак, целые числа это:

• натуральные (1, 2, 3, 4, 5,……..29 далее не имеет конца);
• целые отрицательные числа (-1, -2, -3, -4, -5,…. -29 и до бесконечности);
• 0 (нуль).

Линия из целых чисел будет выглядеть следующим образом ∞…,-3, -2, -1, 0, 1, 2, 3. ∞, где ∞ — это символ бесконечности. Справа от 0 располагаются натуральные, а слева поселились целые отрицательные числа.

• в группе целых, нет самого большого и самого маленького числа, ряд безграничен в обе стороны;
• поддаются сложению, умножению, вычитанию и в результате всегда будет целое число.

На рисунках отмечаются знаком Z.

Целое и натуральное может быть представлено дробью, где «m» – это целое, «n» — это натуральное. Например, 6=6/1. Такие числа являются рациональными.

К ним относятся:

• дроби (2/5);
• десятичные дроби (0,48 = 48/100 или -0125 = -125/1000);
• смешанные (2 целых 5/10);
• целое число, представленное дробью (8=8/1);
• 0 в виде дроби (0/1).

Числа, о которых идёт речь, обладают свойствами:

• сумма двух противоположных чисел равняется 0 (-72+72=0);
• если умножить рациональное число на 1, получим это же число (-1,78*1= -1,78);
• перемножение чисел с разными знаками в результате даст отрицательное число (-3*20=-60);
• при умножении двух отрицательных чисел, в результате получится положительное ((-7)*(-35)=245);
• произведение рационального числа и 0 равняется 0 (0*1/5=0).

Совокупность таких чисел отмечается меткой Q.

Свойства натуральных чисел

Сложение, вычитание, умножение и деление подчиняются законам арифметики. Всего этих законов, основанных на свойствах натуральных чисел, пять.

1. Переместительный закон сложения.

При сложении можно менять порядок слагаемых чисел как угодно — результат всегда будет одинаковым.

5 + 7 = 12 и 7 + 5 = 12

24 + 6 + 8 = 38 и 6 + 24 + 8 = 38 и 8 + 6 + 24 = 38

2. Переместительный закон умножения.

При умножении можно менять порядок множителей как угодно — результат всегда будет одинаковым.

2 х 4 = 8 и 4 х 2 = 8

4 х 3 х 5 = 60 и 3 х 5 х 4 = 60 и 5 х 4 х 3 = 60

3. Сочетательный закон сложения.

При сложении трёх чисел можно сложить первое и второе, и к их сумме прибавить третье, а можно сложить второе и третье, и к их сумме прибавить первое — результат будет один и тот же.

(5 + 7) + 8 = 12 + 8 = 20 и 5 + (7 + 8) = 5 + 15 = 20

17 + (4 + 23) = 17 + 27 = 44 и (17 + 23) + 4 = 40 + 4 = 44

4. Сочетательный закон умножения.

Когда умножаем три числа, то результат не изменится, если перемножать множители не по порядку.

3 х (2 х 5) = 30 и (3 х 5) х 2 = 30

5. Распределительный закон.

Результат умножения суммы на число будет равен результату сложения произведений каждого слагаемого суммы на это число.

5 х (3 + 4) = 5 х 3 + 5 х 4 = 35

Вот мы и познакомились с основной информацией о натуральных числах. Мы используем их каждый день: считаем, сколько ложечек сахара положить в чай, сколько бензина залить в машину. С помощью натуральных чисел мы определяем, что выгодней: купить три маленьких коробочки с печеньем или одну большую. Вычисляем, на сколько долек разрезать яблоко, чтобы угостить сестру, маму, папу — и полакомиться самому. Поэтому обязательно учитесь пользоваться натуральными числами — и они обязательно ещё не раз сослужат вам добрую службу.

Знания лучше всего закрепляются в памяти, если ребёнок применяет их на практике, выполняя интересные задания. Такую возможность предоставляет образовательная платформа iSmart. Здесь представлены онлайн-тренажёры, разработанные в соответствии с образовательными стандартами РФ, являющиеся эффективным вспомогательным инструментом для усвоения школьной программы.

Есть разделы по математике, русскому и английскому языкам, окружающему миру, логике и другим предметам. Кроме упражнений для закрепления материала есть также возможность подготовиться к ВПР и контрольным работам. 

Зарегистрируйте своего ребёнка на образовательной платформе iSmart, чтобы начать занятия.

Натуральные числа: что это и как их использовать

Основное применение натуральных чисел — подсчет и измерение количества объектов в реальном мире. Например, они используются в математике для решения задач на сочетания и перестановки, а также в алгебре для работы с множествами и отношениями.

Натуральные числа также широко применяются в науке и технике. Например, в физике для описания количественных свойств объектов и явлений, в химии для измерения массы и количества вещества, а в программировании для работы с циклами и итерациями.

Важно отметить, что натуральные числа не включают нуль, исключение составляют некоторые определения, в которых ноль также является натуральным числом. Например, в некоторых странах ноль считается первым натуральным числом

Примеры натуральных чисел	Применение
1, 2, 3, 4, 5	Подсчет объектов, математические операции
10, 20, 30, 40, 50	Измерение количества, прогнозирование
100, 200, 300, 400, 500	Наука и техника, статистика

Что такое множество в математике и как оно обозначается

Разряды и классы

Для начала скажем, что при счете мы обычно применяем десятичную систему исчисления. Она подразумевает то, что 10 единиц низшего разряда образуют 1 единицу более старшего, и данная закономерность сохраняется до конца счета.Разрядные единицы – это такие символы, которые обозначают начало определенного разряда.Пример: 1, 10, 100 и т.д.Благодаря разрядным единицам, можно сделать запись менее длинной и более упрощенной.Пример: Записать 298 481 в виде суммы разрядных слагаемых.Решение: 200 000 + 90 000 + 8 000 + 400 + 80 + 1.
Если число состоит из одного знака, то оно называется однозначным. Соответственно – различают двузначные, трехзначные, четырехзначные и т.д.Теперь стоит немного рассказать и о натуральных классах.При чтении определенного числа его разделяют на классы, включающие по три разряда. Первые три единицы представляют собой класс единиц, следующие три – класс тысяч. Далее идут довольно крупные группы – классы миллионов, миллиардов и другие. Помните, что каждая цифра любого класса является разрядом, то есть классы состоят из разрядов.Сравнивать их можно через классы или разряды. Соответственно – то число, где количество старших разрядов преобладает, является более крупным по значению.

Порядок решения – пример

Итак, после подробного разбора основных арифметических операций рассмотрим алгоритм выполнения всех указанных действий в одном равенстве. Возьмем какой-нибудь пример, включающий в себя большинство всех представленных выше взаимодействий.(36 + 76) х (85 – 80) + 96 ÷ 3 = Сначала необходимо выполнить те действия, которые расположены в скобках, то есть требуется раскрыть скобки слева направо. Раскроем скобки в нашем примере и получим следующее выражение:112 х 5 + 96 ÷ 3 = Далее также слева направо выполняем все действия умножения и деления, соответственно – мы получим следующую сумму:560 + 32 = Наконец, производим финальное действие – сложение:592 – конечный результат.Таким образом, мы узнали, что натуральные числа – это все целые и положительные числа, нуль не является таковым

Вникли в небольшую предысторию данных символов и поняли их важное значение в математике. Произвели разбор основных свойств и арифметических действий, производимых с ними

Также рассмотрели алгоритм действий, необходимых для вычисления ответа.Чтобы проверить свои знания по изученной теме, рекомендуем вам пройти тест, представленный ниже, а также посмотреть видео, где вы найдете еще больше примеров решения различных уравнений с натуральными числами.

Десятичная запись натурального числа

Любое, даже самое большое число, можно записать с помощью десяти арабских цифр. Никакие дополнительные символы использовать не нужно. Цифры записываются в строчку, слева направо. Последовательность цифр в одном числе может быть абсолютно любой. Бывают и такие числа, в написании которых цифры повторяются.

Ноль, хоть и не является сам по себе натуральным числом, может применяться для обозначения других натуральных чисел.

Рассмотрим примеры:

1 876 542 — один миллион восемьсот семьдесят шесть тысяч пятьсот сорок два. Достаточно большое число, и для его обозначения понадобились только арабские цифры.

373 — триста семьдесят три. Число, для обозначения которого мы дважды использовали цифру 3.

208 — двести восемь. Число, для обозначения которого мы использовали 0. 

А вот примеры неправильного применения цифры 0:

07, 011, 0117

Ноль означает пустоту, поэтому его не нужно ставить перед числом.

Примечание: ноль перед числом используется для написания дат: 03.05.2022, 07.10.1981. Это делается, чтобы избежать путаницы. 

Практика:

Попросите ребёнка записать с помощью цифр следующие числа: двадцать два, сто восемьдесят семь, пятьсот три, девятнадцать. 

Главные свойства

Рассмотрим основные свойства, которые характерны для всех натуральных чисел. Они применимы всегда и везде, так как способствуют упрощению некоторых выражений различных типов. Их используют при различных вычислениях и преобразованиях.

Свойство 1

От перемены места слагаемых сумма не меняется.Пример: 2 + 1 = 1 + 2 = 3. Как бы мы не переставляли слагаемые, сумма все равно останется такой же.

Свойство 2

От перемены места множителей произведение не меняется.Пример: 2 х 1 = 1 х 2 = 2. Аналогичное правило есть и в умножении. Значение произведения в итоге остается тем же.

Свойство 3

Чтобы прибавить к числу сумму двух других чисел, можно сначала произвести сложение одного числа, а затем – второго.Пример : 2 + (3 + 10) = 3 + (2 + 10) = 15. Данное правило еще называется сочетательным свойством.

Свойство 4

Чтобы умножить на число произведение двух других чисел, можно сначала произвести умножение одного числа, а затем – второго.Пример: 5 х (6 х 4) = (5 х 6) х 4 = 120. Правило, аналогичное предыдущему, только здесь используется другой вид арифметических действий. Принцип остается тем же.

Свойство 5

Для того, чтобы умножить сумму натуральных чисел на другое число, нужно умножить это число на каждую из представленных слагаемых, а затем сложить полученные произведения чисел.Пример: 5 х (4 + 3) = 5 х 4 + 5 х 3 = 35. Это правило умножения числа относительно сложения двух других. Часто применяется в решении заданий по преобразованию каких-либо выражений.Мы выяснили и разобрали на примерах самые главные свойства натуральных чисел

Если вы их не знали раньше, то советуем вам обратить на них особое внимание. А теперь перейдем к изучению наиболее распространенных и часто используемых операций.

Математические операции

Как целые, так и натуральные числа подвержены математическим операциям, но некоторые из них имеют некоторые особенности. Вот некоторые из основных операций, которые могут выполняться с целыми и натуральными числами:

Сложение: Эта операция позволяет складывать два числа, чтобы получить их сумму. Так, например, если у нас есть два натуральных числа 5 и 3, их сумма составит 8. Если у нас есть два целых числа -2 и 4, их сумма составит 2.

Вычитание: Эта операция позволяет вычитать одно число из другого. Например, если мы вычтем из натурального числа 10 число 7, мы получим 3. Если мы вычтем из целого числа -5 число 3, мы получим -8.

Умножение: Эта операция позволяет умножать одно число на другое. Например, если мы умножим натуральное число 4 на 2, мы получим 8. Если мы умножим целое число -3 на 5, мы получим -15.

Деление: Эта операция позволяет делить одно число на другое. При делении натуральных чисел результатом всегда будет натуральное число или десятичная дробь. Например, если мы разделим 10 на 2, мы получим 5. Если мы разделим целое число -15 на 3, мы получим -5.

Возведение в степень: Эта операция позволяет возводить число в определенную степень. Например, если мы возведем натуральное число 2 в степень 3, мы получим 8. Если мы возведем целое число -2 в степень 2, мы получим 4.

Извлечение корня: Эта операция позволяет извлекать корень числа. Извлечение корня является обратной операцией к возведению в степень. Например, если мы извлечем квадратный корень из натурального числа 9, мы получим 3. Если мы извлечем квадратный корень из целого числа 16, мы получим 4.

Отметим, что при выполнении некоторых операций с целыми числами могут возникать особенности, связанные с наличием нуля и отрицательных чисел.