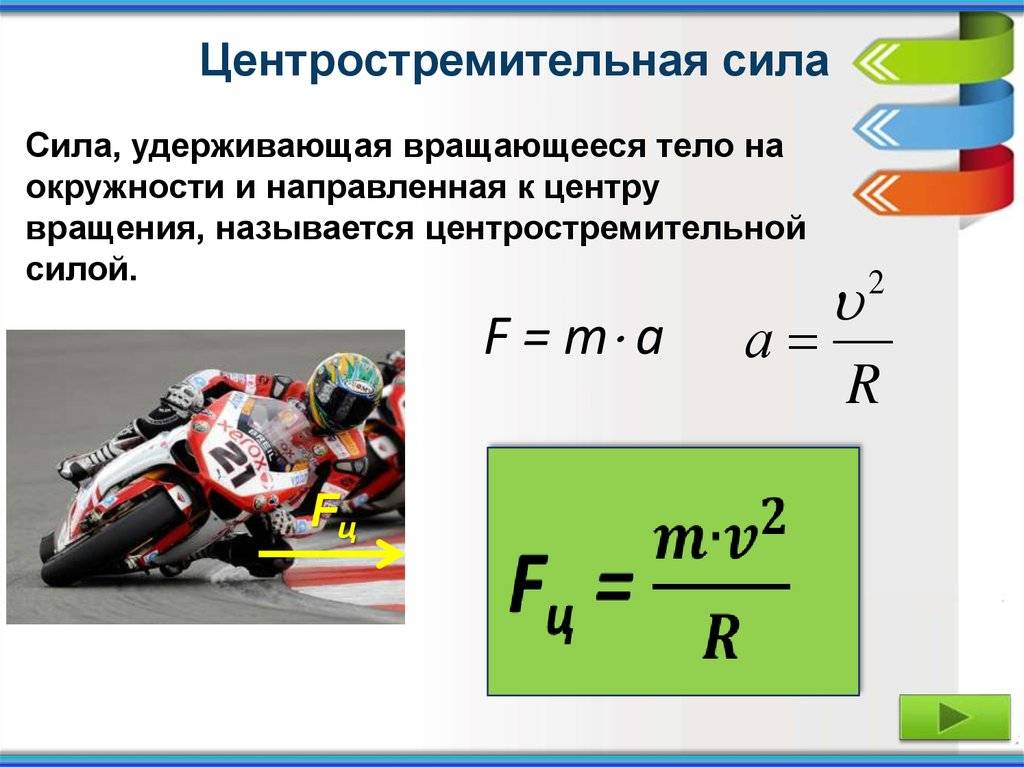
В чем разница между центробежной и центростремительной силой

What is Centrifugal Force?

Sir Christian Huygens first developed the theory of centrifugal force. This theory was developed in the year 1659. The theory of centrifugal force is actually the opposite force of the centripetal force.

The centripetal force is the Newtonian force in which the force on an object is towards the centre of the rotating object. The centrifugal force emerges due to the inertia of the rotating object.

As per Newton’s law, the centripetal force should have an opposite force. This led to the existence of the centrifugal force.

This centrifugal force can also be termed as a frictional force as it works in the opposite direction to that of centripetal force. This is not a real force; this is the inertia of the effect of the body moving.

This force tends to flee the object towards the outer field more than that of the orbit. For example, the graviton is a ride present in some amusement parks.

In this ride, the rider enjoys the feeling of fleeing outside the orbit. This is one of the examples of centrifugal force.

Примеры применения центробежной и центростремительной силы в жизни

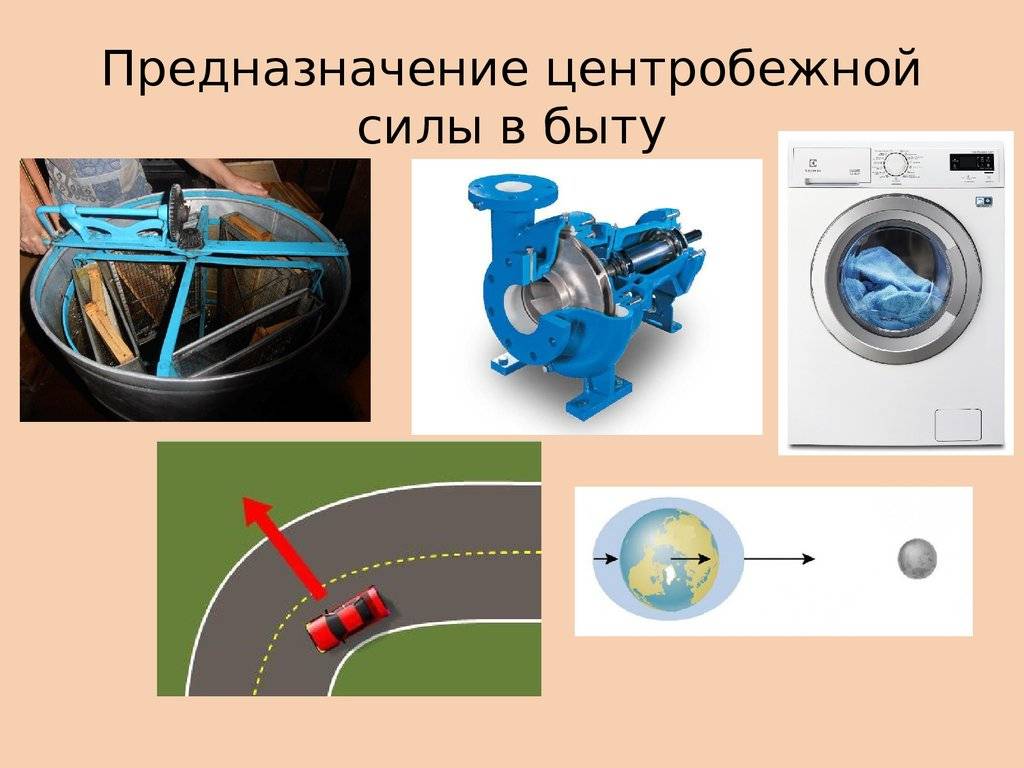
Центробежная и центростремительная силы играют значительную роль в различных аспектах человеческой жизни. Вот некоторые примеры их применения:

1. Аттракционы и горки

Центробежная сила используется в аттракционах и горках для создания ощущения адреналина и веселья. При движении на аттракционах, таких как карусели или паровозики, центробежная сила дает людям ощущение ускорения и выталкивает их от центра вращения. Это создает эффект гравитации и делает поездку более захватывающей.

2. Вращающиеся машины и электроинструменты

Вращающиеся машины, такие как дрели, шлифовальные машины и станки, используют центробежную силу для увеличения эффективности и точности работы. Путем увеличения скорости вращения, эти инструменты создают центробежную силу, которая помогает удалять материал и выполнять различные задачи с большей эффективностью.

3. Циклические спортивные виды

Центростремительная сила является ключевым элементом в спортивных дисциплинах, таких как гимнастика, фигурное катание и велосипедизм. При выполнении вращательных движений, спортсмены ощущают центростремительную силу, которая позволяет им сохранять баланс, выполнять трюки и обеспечивает необходимую поддержку и стабильность.

4. Центрифуга

Центробежная сила играет критическую роль в работе центрифуги. Центрифуга используется для разделения жидкости и твердых частиц, основываясь на разных центробежных силах, которые действуют на разные компоненты смеси. Это позволяет проводить различные анализы и эксперименты в научных и медицинских лабораториях.

5. Мессеровщики и экстрим-спортсмены

Центростремительная сила применяется в специальных спортивных дисциплинах, таких как мессеровщики и экстрим-сопротивления. Во время трюков и вращательных движений, спортсмены используют центростремительную силу, чтобы создавать динамические и захватывающие маневры, добавляя сложность и эффект в исполнении.

В целом, понимание центробежной и центростремительной силы помогает нам объяснить и оценить различные аспекты жизни, связанные с движением и вращательными процессами. Эти силы имеют широкий спектр применений, от развлечений до научных исследований, и играют важную роль в нашем повседневном опыте.

Приложения

В повседневных процессах движения центростремительная сила часто передается через . В случае трения скольжения сила трения направлена против скорости скольжения и не допускает управляемого движения. Центростремительное ускорение должно выполняться при следующем условии:

аZп≦μ⋅грамм{\ Displaystyle а_ {Zp} \ leqq \ mu \ cdot g}

с коэффициентом статического трения и ускорением свободного падения . Исследования показывают, что центростремительное ускорение в 4 м / с 2 редко превышается при нормальном вождении автомобиля . В случае мотоцикла это соответствует уклону около 20 градусов. Это все еще далеко от физических ограничений на сухой дороге, но это показывает, что люди могут регулировать свою скорость таким образом, чтобы произведение квадрата скорости движения и кривизны оставалось в указанных пределах.
μ{\ displaystyle \ mu}грамм{\ displaystyle g}

Для многих задач определение радиуса кривизны может быть упрощено. Если внешние силы известны, уравнение движения обеспечивает ускорение, скорость и положение центра масс. Поезд, например B. движение центра тяжести транспортного средства рассматривается в проекции на контрольную поверхность. В этом случае составляющая ускорения, перпендикулярная скорости, является искомым центростремительным ускорением. В простейшем случае опорной поверхностью является плоскость xy инерциальной системы отсчета.
а→знак равноФ.→м{\ displaystyle {\ vec {a}} = {\ vec {F}} / м}

В эксперименте ускорение обычно измеряется в компонентах фиксированной системы координат транспортного средства. Чтобы получить ускорение, параллельное базовой плоскости, необходимо скорректировать часть ускорения свободного падения, которая измеряется в поперечном направлении из-за угла крена .

Что общего между ними

Пришло время сравнить центробежную и центростремительную силы. У них есть отличия и сходства. Вот общие черты:

Равны по значению

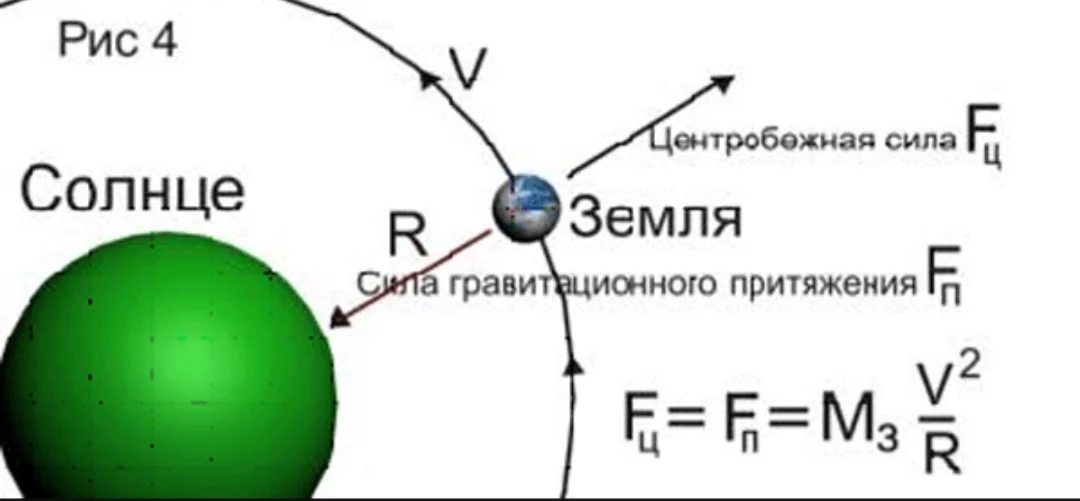
Земля кружится вокруг Солнца по эллиптической орбите. Когда планета пролетает на расстоянии 147 миллионов километров, её скорость равна 30,2 км/с. Этот участок называется перигелий. Здесь F_цб больше всего, потому что скорость выше средней, а промежуток между планетой с центром вращения короткий.

На расстоянии в 152 миллиона километров до Солнца скорость падает до 29,2 км/с. Эта зона называется афелием. Здесь F_цб самая низкая, потому что дистанция до звезды больше, а скорость ниже средней.

Между перигелием и афелием планета летит со средней скоростью 29,8 км/с.

Возникают одновременно

Они появляются, когда предмет движется криволинейно. Вот примеры для наглядности:

В лопасти конструкции с электромотором повесили два груза. Мотор закрутил их, появилась инерция. Они начали кружиться на лопастях, но не улетели. Их удержала F_цс.

Автомобиль разогнался до 120 км/ч и пошёл в вираж. Машину занесло, она поменяла направление движения за счёт F_цб. Но автомобиль не вылетел с дороги и остался на полосе. Так получилось, потому что F_цс удержала машину.

Во всех примерах они стали действовать одновременно.

Уравнение центробежной силы

Поскольку центробежная сила является псевдосилой или ощущением, нам сначала нужно вывести уравнение для центростремительной силы. Помните, что обе эти силы равны по величине, но противоположны по направлению.

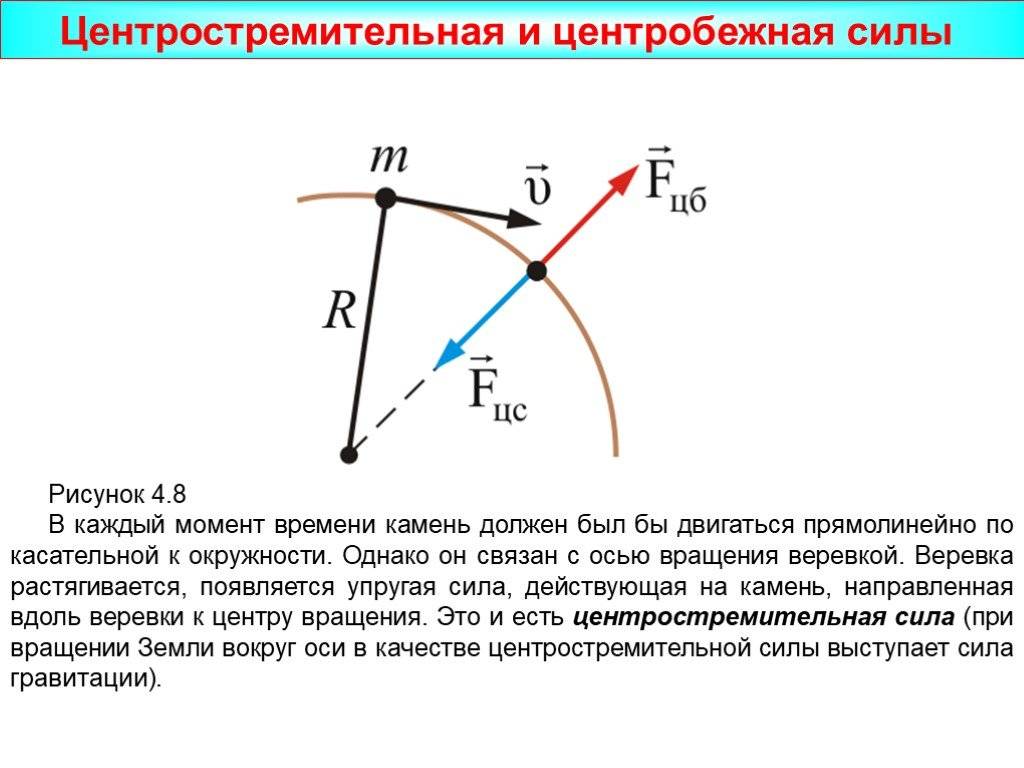
Представьте себе камень, привязанный к струне, который вращается с равномерной скоростью. Пусть длина струны равна $r$, то есть она также равна радиусу круговой траектории. Теперь сфотографируйте этот камень, который вращается. Интересно отметить следующее. величина тангенциальной скорости камня будет постоянной во всех точках кругового пути Однако направление тангенциальной скорости будет постоянно меняться. Так что же такое эта тангенциальная скорость?

Тангенциальная скорость определяется как скорость объекта в данный момент времени, действующая в направлении, касательном к траектории его движения.

Вектор касательной скорости будет направлен по касательной к круговому пути, пройденному камнем. При вращении камня этот вектор касательной скорости постоянно меняет свое направление.

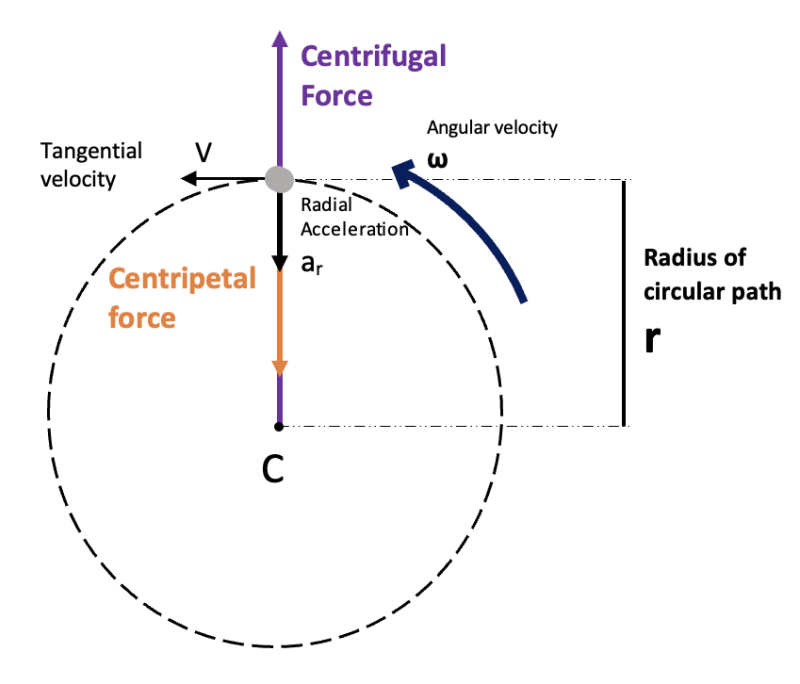
А что значит, если скорость продолжает меняться, камень ускоряется! Теперь, согласно Первый закон Ньютона о движении n Но что это за сила, которая заставляет камень двигаться по круговой траектории? Вы, наверное, помните, что когда вы вращаете камень, вы, по сути, натягиваете струну, создавая напряжение, которое приводит к возникновению силы притяжения камня. Именно эта сила и ускоряет камень по круговой траектории.И эта сила известна как Центростремительная сила .

Величина центростремительной или радиальной силы определяется вторым законом движения Ньютона: $$\overset\rightharpoonup{F_c}=m\overset\rightharpoonup{a_r},$$$

где $F_c$ – центростремительная сила, $m$ – масса объекта и $a_r$ – радиальное ускорение.

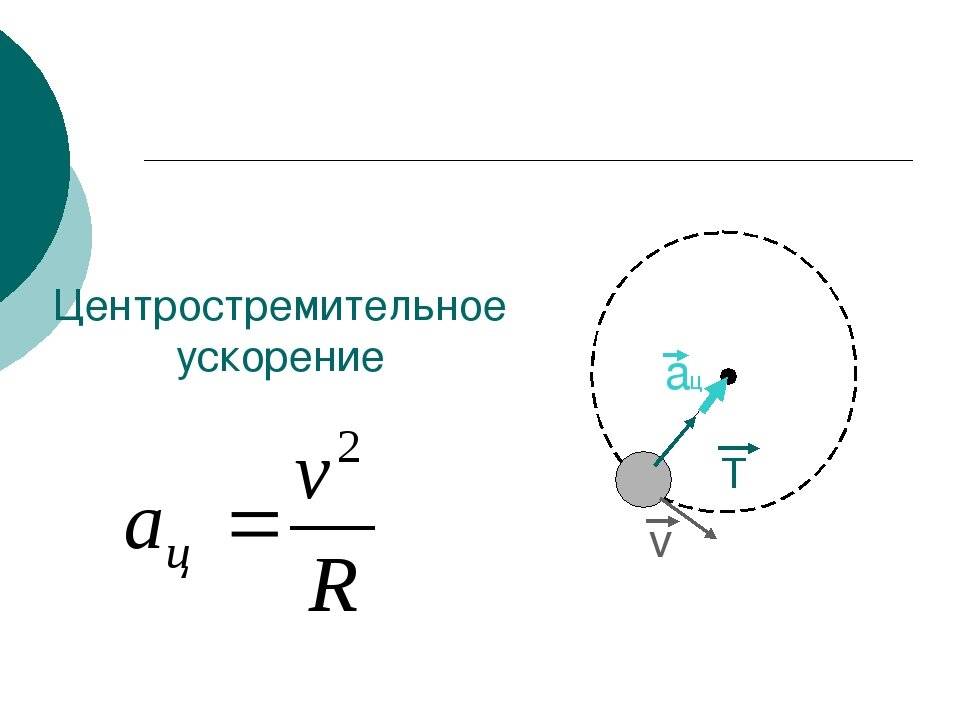
Каждый объект, движущийся по окружности, имеет радиальное ускорение. Это радиальное ускорение можно представить в виде: $$\overset\rightharpoonup{a_r}=\frac{V^2}r,$$

где $a_r$ – радиальное ускорение, $V$ – тангенциальная скорость и $r$ – радиус круговой траектории.

Объединив это с уравнением для центростремительной силы, получим $$\overset\rightharpoonup{F_c}=\frac{mV^2}r$$.

Тангенциальная скорость также может быть представлена в виде :$$V=r\omega$$

$$\mathrm{Tangential}\;\mathrm{velocity}\operatorname{= }\mathrm{angular}\;\mathrm{velocity}\times\mathrm{radius}\;\mathrm{of}\;\mathrm{circular}\;\mathrm{path}$$.

Это дает другое уравнение для центростремительной силы: $$\overset\rightharpoonup{F_c}=mr\omega^2$$$.

Но подождите, это еще не все! Согласно третьему закону движения Ньютона, каждое действие имеет равную и противоположную реакцию. Что же тогда может действовать в направлении, противоположном центростремительной силе? Это не что иное, как центробежная сила. Центробежную силу называют псевдосилой, потому что она существует только благодаря действию центростремительной силы. Центробежная сила будет иметь величину, равнуюцентростремительной силы в противоположном направлении, что означает, что уравнение для расчета центробежной силы также:

$$\overset\rightharpoonup{F_c}=mr\omega^2$$$.

где масса измеряется в $\mathrm{kg}$, радиус в $\mathrm{m}$ и $\omega$ в $\text{radians}/\text{sec}$. Давайте теперь используем эти уравнения в нескольких примерах.

Прежде чем использовать единицу угловой скорости в уравнении, нам нужно перевести ее из градусов/сек в радианы/сек. Это можно сделать с помощью следующего уравнения $\mathrm{Deg}\;\times\;\pi/180\;=\;\mathrm{Rad}$

Понятие силы в физике

Сила имеет несколько основных характеристик:

Величина: Сила измеряется в ньютонах (Н).

Направление: Силы могут действовать в разных направлениях, и это направление важно при определении их влияния на объект.

Точка приложения: Сила может быть приложена к объекту в разных точках, и это также влияет на результат ее действия.

Сила может вызывать изменение состояния движения объекта: замедление, ускорение, изменение направления движения или остановку. Все эти эффекты зависят от силы, ее направления и точки ее приложения.

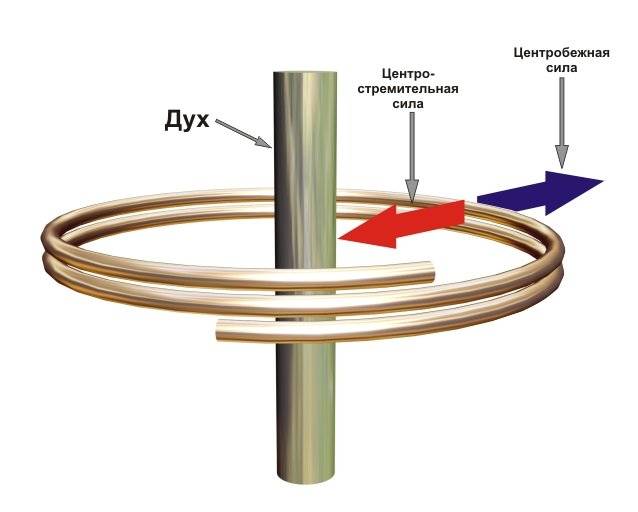
В физике выделяют два основных типа сил: центробежную силу и центростремительную силу.

Центробежная сила — это сила, действующая на объект, движущийся по окружности. Она направлена от центра окружности и перпендикулярна к направлению движения объекта.

Центростремительная сила, наоборот, направлена к центру окружности и вдоль направления движения объекта.

Эти два типа сил очень похожи, но отличаются своим направлением. Оба типа сил могут быть применены к объекту, чтобы вызвать его движение по окружности.

Понимание понятия силы и ее типов помогает в объяснении многих физических явлений и является основой механики.

Превышение запаса прочности

В предыдущем опыте мы имели дело с идеальной веревкой, которая не рвалась. Но, допустим, наша веревка самая обычная, и даже можно вычислить усилие, после которого она просто порвется. Для того чтобы рассчитать эту силу, достаточно сопоставить запас прочности веревки с нагрузкой, которую она испытывает в процессе вращения камня. Вращая камень с большей скоростью, вы сообщаете ему большее количество движения, а значит, и большее ускорение.

При диаметре джутовой веревки около 20 мм ее прочность на разрыв равна около 26 кН. Примечательно, что длина веревки нигде не фигурирует. Вращая груз размером в 1 кг на веревке радиусом в 1 м, можно вычислить, что линейная скорость, необходимая для ее разрыва равна 26 х 10 3 = 1кг х V 2 / 1 м. Таким образом, скорость, которую опасно превышать, будет равна √26 х 10 3 = 161 м/с.

Инерция движущегося тела

Движущееся тело обладает инерцией, то есть оно продолжает двигаться по инерции даже после прекращения действия внешней силы на него. Это объясняется тем, что тело сохраняет свою кинетическую энергию.

Инерция движущегося тела проявляется в том, что оно стремится сохранить свое направление и скорость в пространстве. Если на движущееся тело не действуют другие силы, то оно будет продолжать двигаться равномерно и прямолинейно до тех пор, пока не появятся препятствия или внешние силы, изменяющие его состояние движения.

Например, когда автомобиль резко тормозит, пассажиры, находящиеся в салоне, продолжают двигаться вперед по инерции. Если в момент торможения не пристегнуть ремни безопасности, то пассажиры могут получить травмы в результате изменения состояния движения автомобиля.

Инерция движущегося тела позволяет объяснить принцип работы некоторых устройств, таких как реактивные двигатели и вращающиеся механизмы.

Ускорение без изменения скорости

И все же, отчего тело с ускорением, направленным к центру, не движется быстрее и не перемещается ближе к центру вращения? Ответ кроется в самой формулировке ускорения. Факты говорят о том, что движение по окружности реально, но для его поддержания требуется ускорение, направленное к центру. Под действием силы, вызванной данным ускорением, происходит изменение количества движения, в результате чего траектория движения постоянно искривляется, все время меняя направление вектора скорости, но не изменяя ее абсолютной величины. Двигаясь по кругу, наш многострадальный камень устремляется внутрь, в противном случае он продолжал бы двигаться по касательной. Каждое мгновение времени, уходя по касательной, камень притягивается к центру, но не попадает в него. Еще одним примером центростремительного ускорения может стать водный лыжник, описывающий небольшие круги на воде. Фигура спортсмена наклонена; он как бы падает, продолжая движение и наклонившись вперед.

Таким образом, можно сделать вывод о том, что ускорение не увеличивает скорость тела, так как векторы скорости и ускорения перпендикулярны друг к другу. Добавляясь к вектору скорости, ускорение лишь меняет направление движения и удерживает тело на орбите.

Сила Кориолиса

Густав
Кориолис (1792 – 1873) – французский учёный
в области механики.

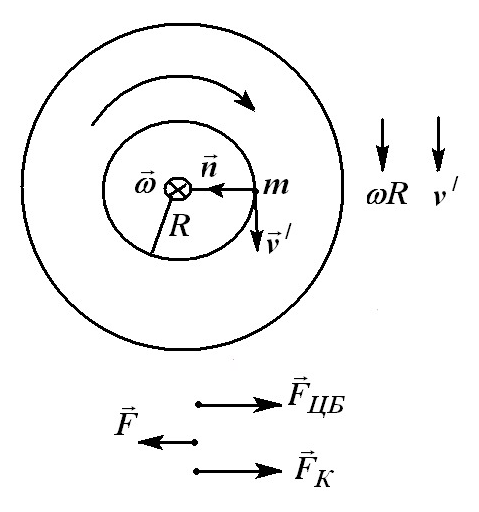
Рис. 2.4

ри движении тела ()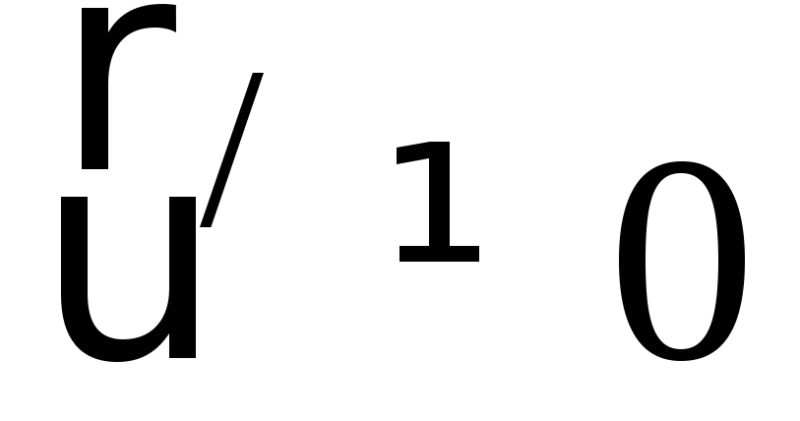
в неинерциальной вращающейся системе
отсчёта кроме центробежной силы возникает
еще одна сила инерции, называемая силой
Кориолиса
.

Возьмём
горизонтально расположенный диск,
вращающийся относительно инерциальной
системы отсчёта с постоянной угловой
скоростью
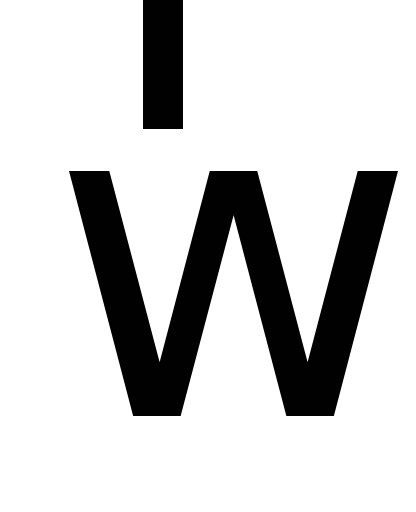(её определение будет в лекции № 3) (рис.
2.4). Допустим, что по окружности радиусомR

равномерно движется привязанная нитью
к оси диска материальная точка (частица)
со скоростью
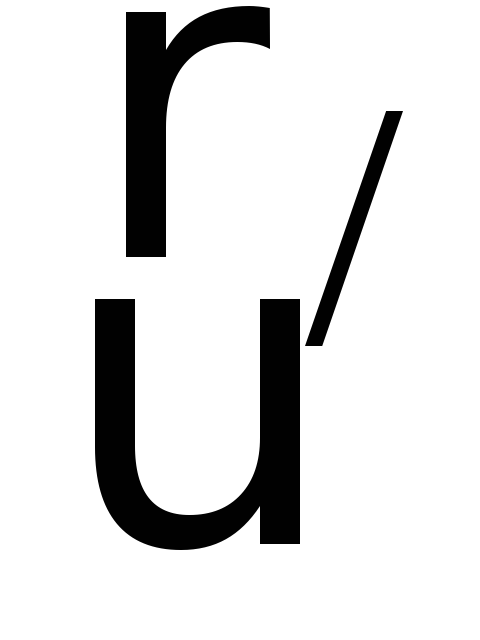относительно диска. Её скорость
относительно Земли имеет модуль.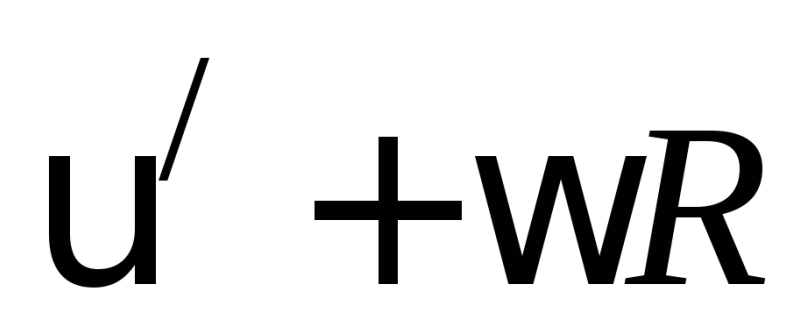

Центростремительное
ускорение:

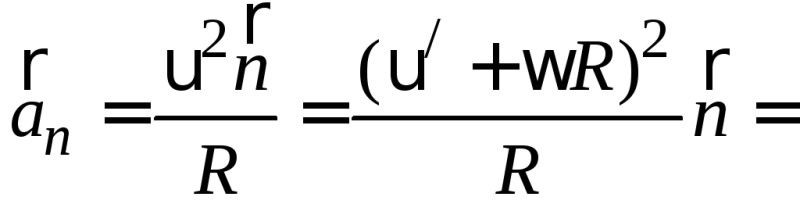
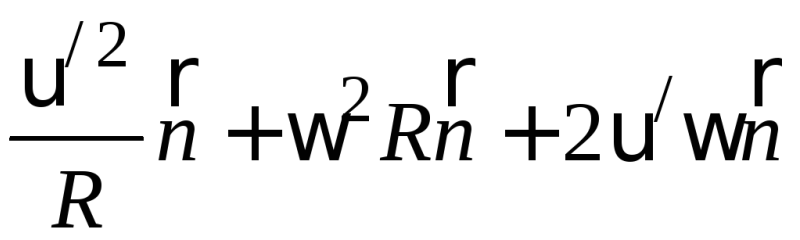Сила
натяжения нити:

где
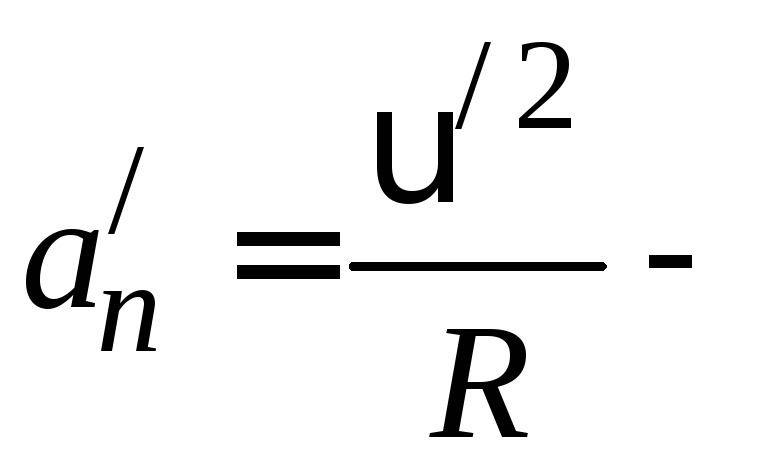ускорение
частицы относительно диска. Перенося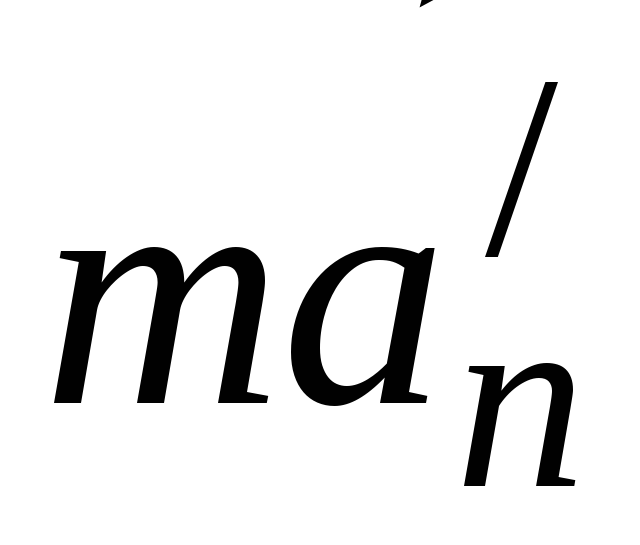в левую часть, а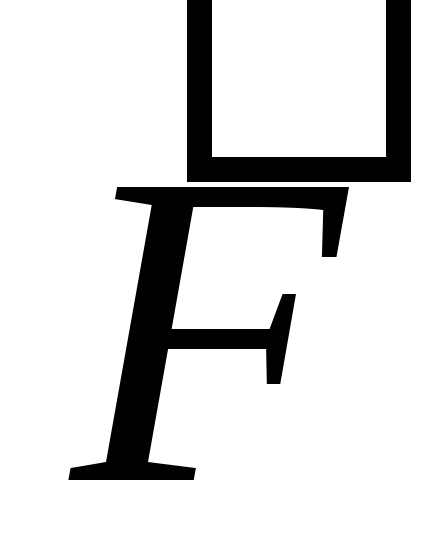в правую, получим:

или

(Формально
это выглядит как 2-й закон Ньютона).

Здесь
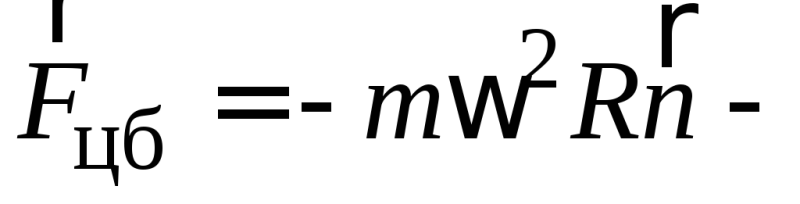центробежная
сила инерции;

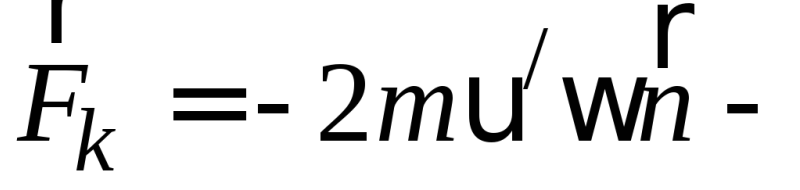сила
Кориолиса, которую можно представить
в виде векторного произведения:

Многие
течения в мировом океане, а также
ветры-пассаты обязаны своим происхождением
силе Кориолиса. Силы Кориолиса необходимо
учитывать при движении ракет и т.д.

5.

Центр инерции.

Определение.

Центром
инерции (центром масс)

системы материальных точек (частиц)
называется точка С,

положение которой задаётся радиус-вектором
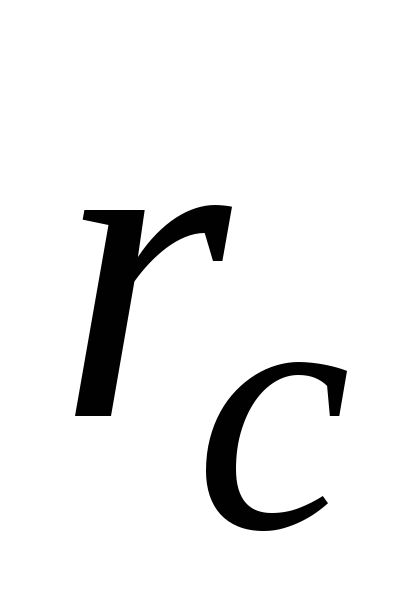, определённым следующим образом:

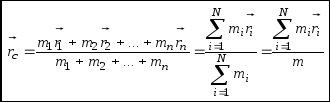
где
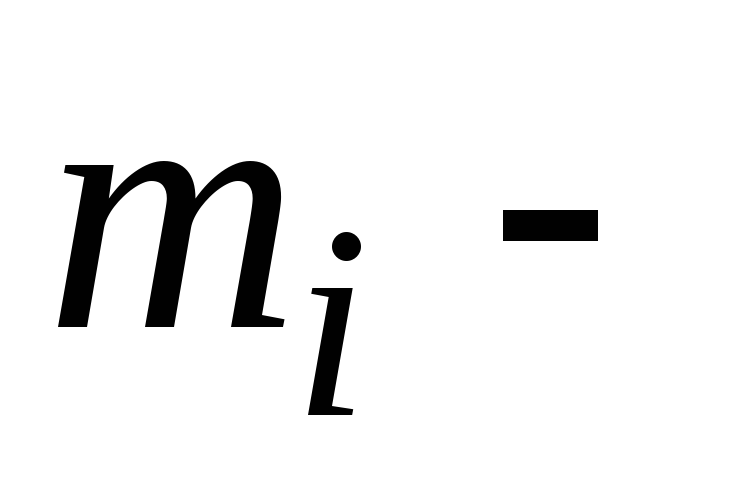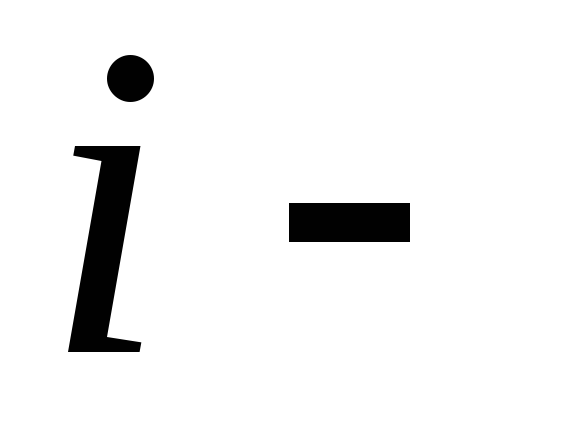массай
частицы;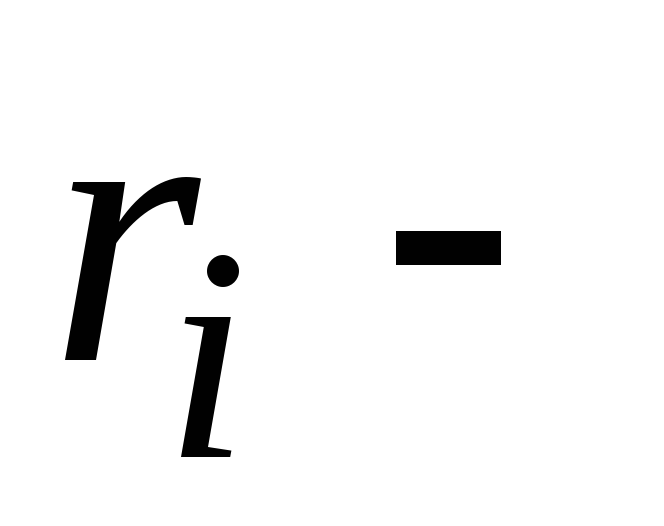радиус-вектор,
определяющий положение этой частицы;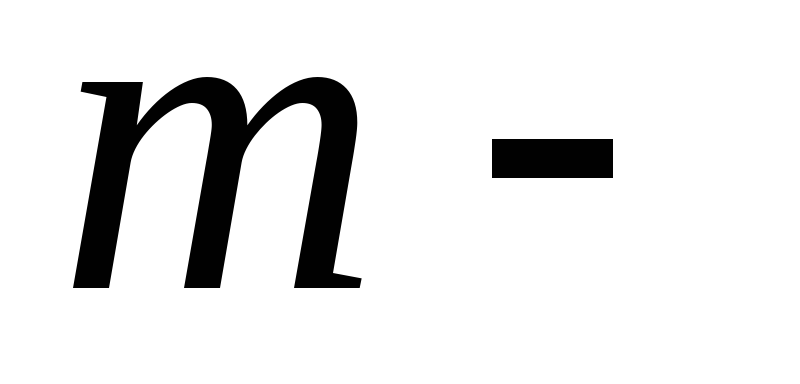масса
системы.

Замечание:
в
однородном поле сил тяжести центр
инерции совпадает с центром тяжести

системы.

Литература

Ньютон И. Математические начала натуральной философии. Пер. и прим. А. Н. Крылова. М.: Наука, 1989
С. Э. Хайкин. Силы инерции и невесомость. М.: «Наука», 1967 г.
Фриш С. А. и Тиморева А. В. Курс общей физики, Учебник для физико-математических и физико-технических факультетов государственных университетов, Том I. М.: ГИТТЛ, 1957
«Центробежная сила» в Большой советской энциклопедии

↑ Ньютон И. Математические начала натуральной философии. Пер. и прим. А. Н. Крылова. М.: Наука, 1989
↑ Ключевым в этой формулировке является утверждение о наличии у предметов материального мира неких волевых качеств, что было в начале формирования научных представлений об окружающем мире весьма распространённым способом обобщения результатов наблюдения за явлениями природы и выяснения свойственных ей общих закономерностей. Примером такого анималистического представления о природе являлся бытовавший в натурфилософии принцип: «Природа боится пустоты», от которого пришлось отказаться после эксперимента Торричелли (Торричеллиева пустота)
↑ В связи с этим Максвелл заметил, что, с таким же успехом можно было бы сказать, что кофе сопротивляется тому, чтобы стать сладким апеллируя к тому, что оно становится сладким не само по себе, а лишь после того, что в него положен сахар.
↑ Ньютон И. Математические начала натуральной философии. Пер. и прим. А. Н. Крылова. М.: Наука, 1989
↑ 1 2 С. Э. Хайкин. Силы инерции и невесомость. М.: «Наука», 1967 г.
↑ При этом в каждый малый момент времени каждое из тел будет приближаться к центру на такое расстояние, какое равно разности расстояний между его траекторией и касательной в точке наблюдения. Иными словами, тела падают друг на друга, но всегда промахиваются.

Фонд Викимедиа. 2010 .

Исторический

Выражение центробежной силы ( по- латыни vis centrifuga ) было открыто Христианом Гюйгенсом в 1659 году, задолго до того , как Исаак Ньютон сформулировал фундаментальный принцип динамики и четко определил общее понятие силы . Открытые им теоремы были опубликованы в 1673 году в качестве приложения к его « часам осциллятора» . Мемуары 1659 года были опубликованы только в 1703 году, примерно через десять лет после его смерти.

Со времен Галилея мы знаем, что тела падают в свободном падении с равномерно ускоренным движением. С точки зрения Гюйгенса, тело притягивает проволоку, которая удерживает ее, когда это тело стремится двигаться в направлении протяжения проволоки с равномерно ускоренным движением. По его словам, это правило применяется не только к тяжелому телу, но и к телу, вращающемуся по кругу на конце проволоки вокруг фиксированной точки. В последнем случае сила тяги, оказываемая на проволоку, противодействует центробежной силе, которая в случае разрыва проволоки отодвигает тело от его круговой траектории, заставляя его следовать по прямолинейной траектории, касательной к окружности. Относительно круга, когда проволока обрывается, расстояние между точкой, занимаемой телом на касательной, и точкой, которую оно занимало бы на окружности, увеличивается при равномерно ускоренном движении. Затем сравнение со свободным падением позволяет Гюйгенсу определить выражение центробежной силы по отношению к весу. В нем, в частности, говорится, что:

Утверждение I: при постоянной угловой скорости центробежная сила пропорциональна радиусу окружности;
Предложение II: при постоянном радиусе оно пропорционально квадрату скорости;
Утверждение V: центробежная сила движущегося тела, пересекающего круг со скоростью, равной скорости, полученной в конце свободного падения на четверть диаметра, равна его весу.

В современных обозначениях утверждение V гласит, что если R – радиус круговой траектории, и если v – скорость, полученная в конце свободного падения с высоты R / 2, (т.е. где g – это l ‘ускорение свободного падения ), то центробежное ускорение равно г либо . Утверждения I и II утверждают, что центробежное ускорение есть во всех случаях.
vзнак равнорграмм{\ displaystyle v = {\ sqrt {Rg}}}v2р{\ displaystyle v ^ {2} / R}v2р{\ displaystyle v ^ {2} / R}

Выражение силы фиктивное появляется у Кориолиса в 1844 году.

Центробежная сила как реальная сила

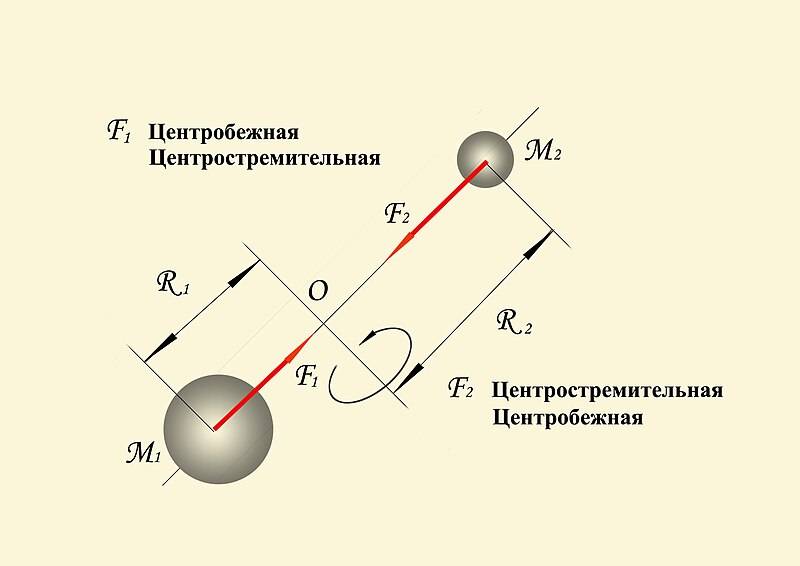
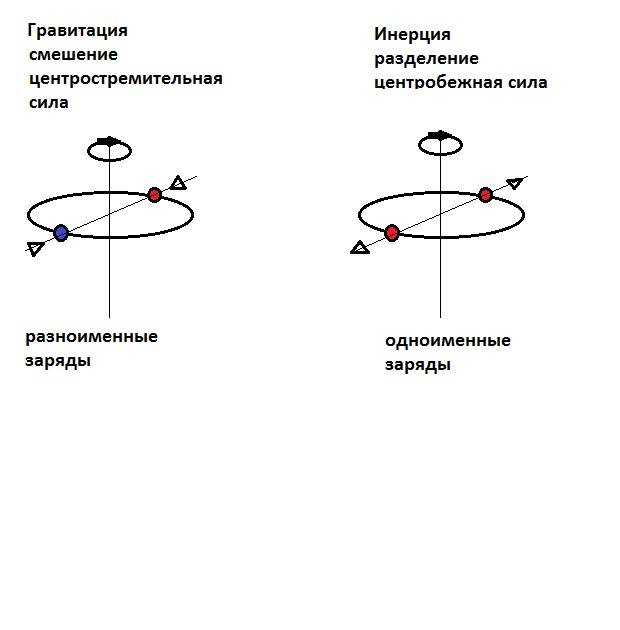
Центростремительная и центробежная силы при движении тел по круговым траекториям с общей осью вращения

Применяемый не к связям, а, наоборот, к поворачиваемому телу, как объекту своего воздействия, термин «центробежная сила» (букв. cила, приложенная к поворачивающемуся или вращающемуся материальному телу, заставляющего его бежать
от мгновенного центра поворота), есть эвфемизм, основанный на ложном толковании первого закона (принципа Ньютона) в форме:

Отголоском этой традиции и является представление о некоей силе
, как о материальном факторе, реализующем это сопротивление или стремление. О существовании такой силы уместно было бы говорить, если бы, например, вопреки действующим силам, движущееся тело сохраняло бы свою скорость, но это не так .

Использование термина «центробежная сила» правомочно тогда, когда точкой её приложения является не испытывающее поворот тело, а ограничивающее его движение связи. В этом смысле центробежная сила представляет собой один из членов в формулировке третьего закона Ньютона, антагониста центростремительной силе, вызывающей поворот рассматриваемого тела и к нему приложенной. Обе эти силы равны по величине и противоположны по направлению, но приложены к разным
телам и потому не компенсируют друг друга, а вызывают реально ощутимый эффект – изменение направление движения тела (материальной точки).

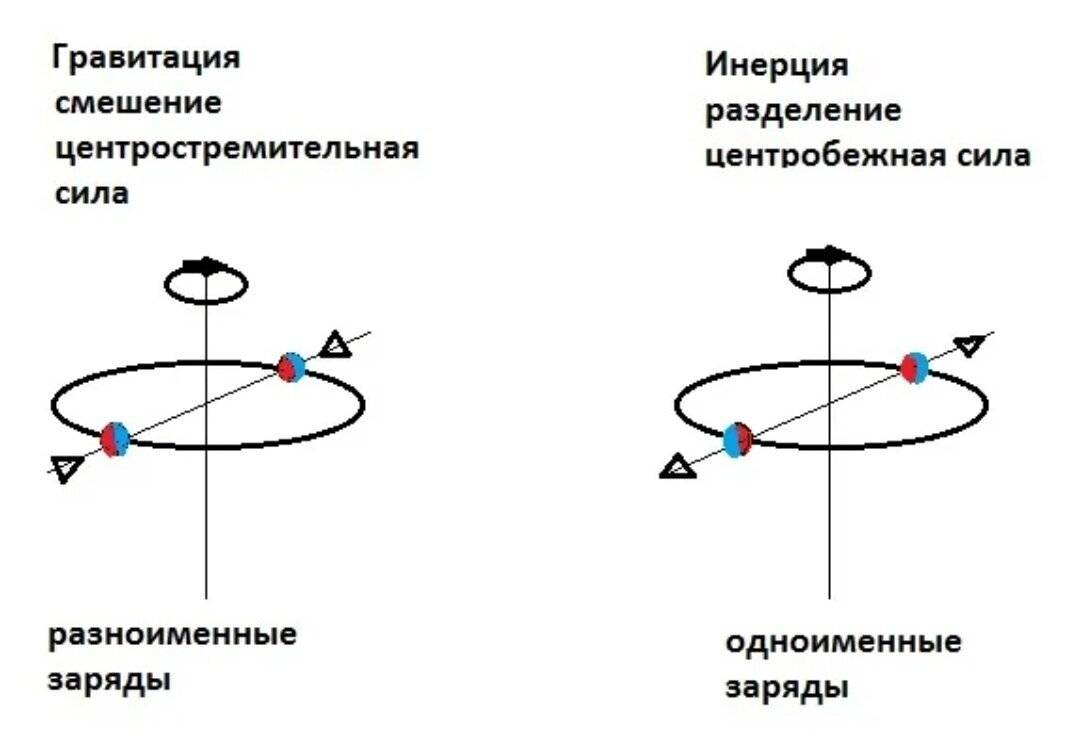
Оставаясь в инерциальной системе отсчёта
, рассмотрим два небесных тела, например, компонента двойной звезды с массами одного порядка величины и , находящихся на расстоянии друг от друга. В принятой модели эти звёзды рассматриваются как материальные точки и есть расстояние между их центрами масс. В роли связи между этими телами выступает сила Всемирного тяготения , где – гравитационная постоянная. Это – единственная здесь действующая сила, она вызывает ускоренное движение тел навстречу друг другу.

Однако, в том случае, если каждое из этих тел совершает вращение вокруг общего центра масс с линейными скоростями = и = , то подобная динамическая система будет неограниченное время сохранять свою конфигурацию, если угловые скорости вращения этих тел будут равны: = = , а расстояния от центра вращения (центра масс) будут соотноситься, как: = , причём , что непосредственно следует из равенства действующих сил: и , где ускорения равняются соответственно: = и .

Центростремительные силы, вызывающие движение тел по круговым траекториям равны (по модулю): =. При этом первая из них является центростремительной, а вторая – центробежной и наоборот: каждая из сил в соответствии с Третьим законом является и той, и другой.

Поэтому, строго говоря, использование каждого из обсуждаемых терминов излишне, поскольку они не обозначают никаких новых сил, являясь синонимами единственной силы – силы тяготения. То же самое справедливо и в отношении действия любой из упомянутых выше связей.

Однако, по мере изменения соотношения между рассматриваемыми массами, то есть всё более значительного расхождения в движении обладающих этими массами тел, разница в результатах действия каждой из рассматриваемых тел для наблюдателя становится всё более значительной.

В ряде случаев наблюдатель отождествляет себя с одним из принимающих участие тел, и потому оно становится для него неподвижным. В этом случае при столь большом нарушении симметрии в отношении к наблюдаемой картине, одна из этих сил оказывается неинтересной, поскольку практически не вызывает движения.

Comparison Table

Parameters of Comparison	Centripetal Force	Centrifugal Force
Definition	This is a force that has the capacity to make an object kept moving around in a circular path.	This is the tendency of the particular object to fly away from the center.
Direction	The force is along the circle’s radius and is directed from the objects to the center.	The force is along the radius, and it is towards the object from the center
Defined by	This theory was first discovered and defined by Sir Isaac Newton	This theory was first discovered and defined Christian Huygens
Status	This is a real force that affects the body moving and keeps the body moving in the circular path	This is not a real force. This is the inertia of the effect of the body moving
Year of discovery	1684	1659

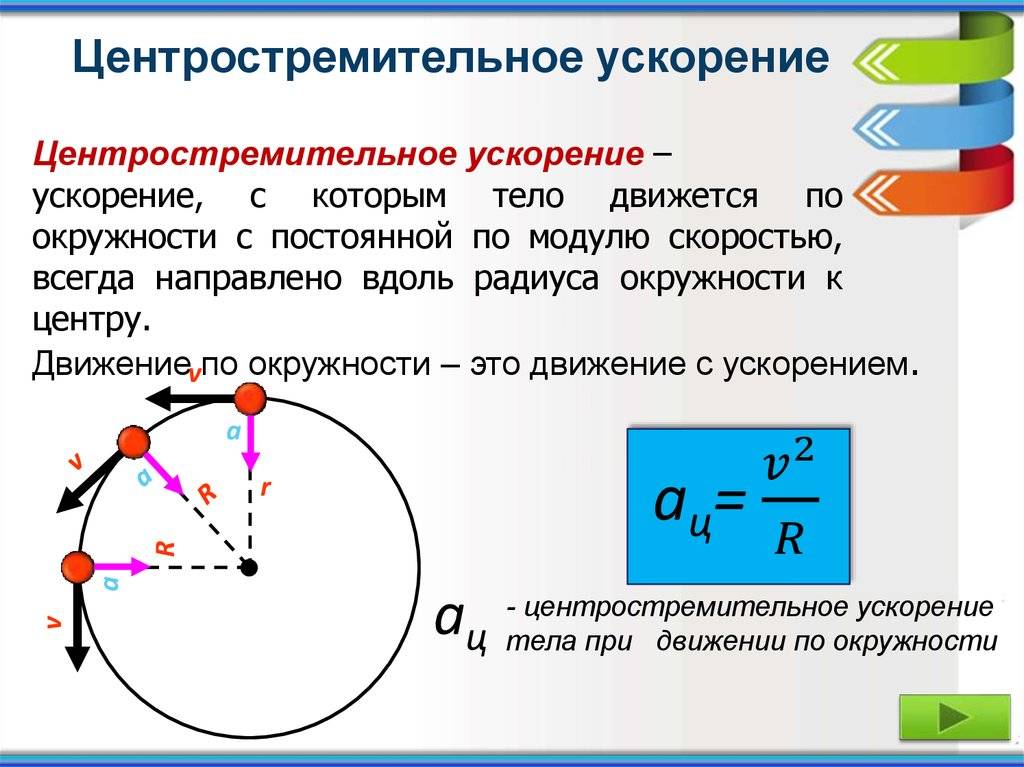
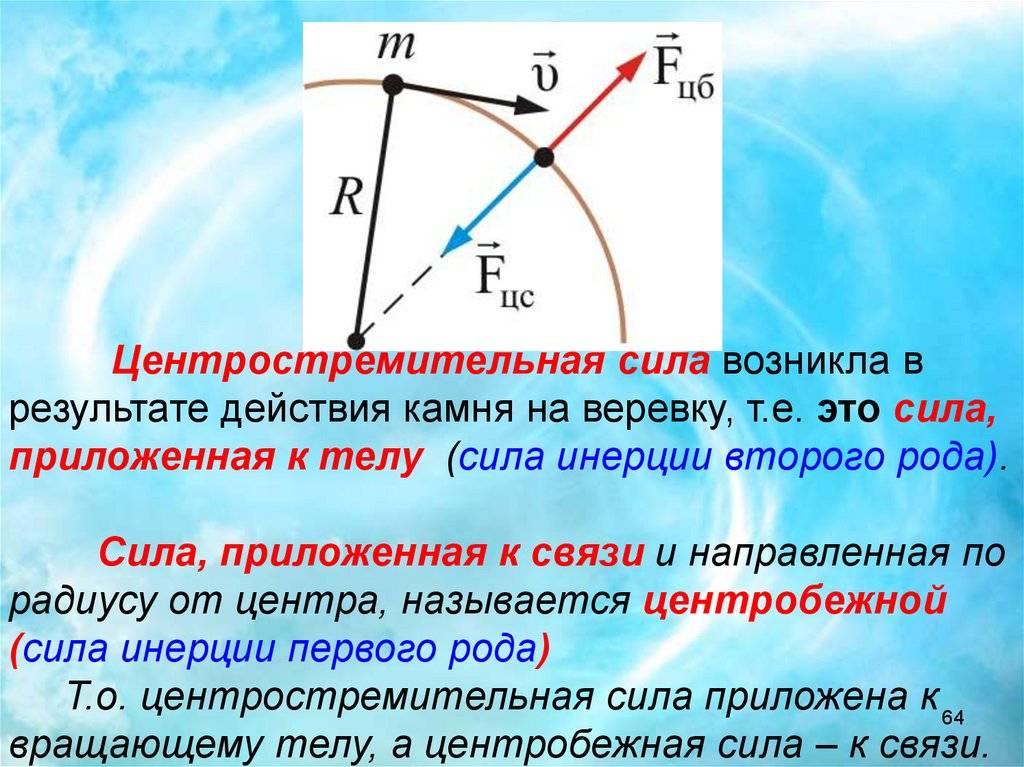
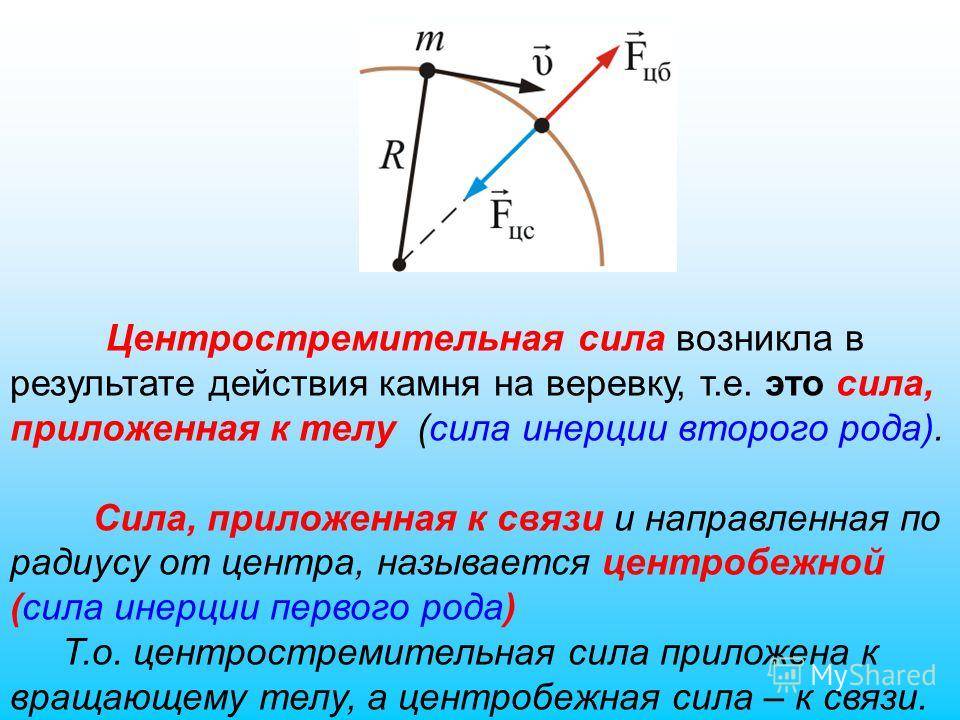
Центростремительная и центробежная силы

Буквально, эти силы как бы направлены определенным образом к центру — точке, равноудаленной от всех точек на пути движущегося тела. В двумерном пространстве (на плоскости) такая орбита является окружностью, а в трехмерном пространстве — окружностью, образованной пересечением поверхности сферы с плоскостью, которая в общем случае не проходит через ее центр. Все остальные орбиты не являются центрированными в этом смысле, и поэтому использование центростремительных и центробежных сил не оправдано и приводит к многочисленным недоразумениям и заблуждениям относительно тел, движущихся по некруговым орбитам.

Центростремительная сила — это сила, действующая на некоторые звенья, которая ограничивает свободу движения тела и заставляет его вращаться вокруг центра вращения. Природа связей может быть произвольной до тех пор, пока они обладают свойством увеличивать потенциальную энергию системы тело-связь с увеличением длины.

Реальной является только сила реакции связи. Центростремительная сила, как и центробежная сила, как самостоятельная сила не существует и является лишь результатом формального разложения реальной силы на две составляющие.

Для тела в постоянном движении (вращении) центростремительная сила совпадает с силой, представляющей реакцию связи; она направлена перпендикулярно вектору скорости, работа не совершается, кинетическая энергия тела не изменяется, и это движение может продолжаться бесконечно.

При переходном движении по кривой (например, при вращении кленового дерева) траектория тела спиральная, а центростремительная сила, которая по определению перпендикулярна касательной к траектории, направлена к мгновенному центру вращения и является результатом типичного разложения реальной силы реакции сцепления на две силы. Тангенциальная составляющая силы реакции сцепления, которая приводит к изменению кинетической энергии тела (в случае ускорения) или к уменьшению (в случае замедления), выполняет определенную функцию. Она происходит периодически во вселенском пространстве во время движения небесных тел по эллиптическим орбитам Кеплера вокруг общего центра тяжести.

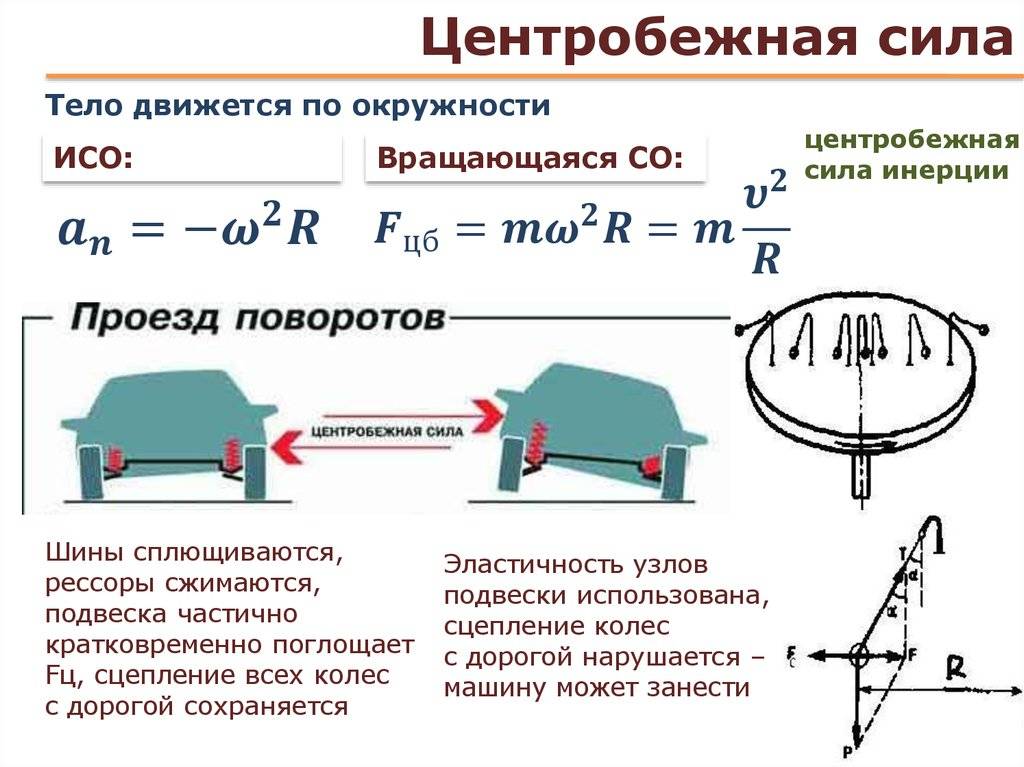
Центробежная сила — это сила, действующая со стороны вращающегося тела на звенья, которые вызывают это вращение. По модулю она равна центростремительной силе и всегда направлена в противоположную сторону (третий закон Ньютона). Термин центробежная сила (буквально: центробежная сила) относится не к звеньям, а к вращающемуся телу как объекту ее действия. Сила, действующая на вращающееся или вращающееся материальное тело, заставляющая его удаляться от мгновенного центра вращения) — это эвфемизм, основанный на неверной интерпретации первого закона Ньютона (принципа Ньютона) 1 в форме :

Отголоском этой традиции является идея силы как материального агента, который реализует это сопротивление или импульс. Существование такой силы было бы уместно, например, если бы движущееся тело сохраняло свою скорость, несмотря на действующие силы, но это не так. 3

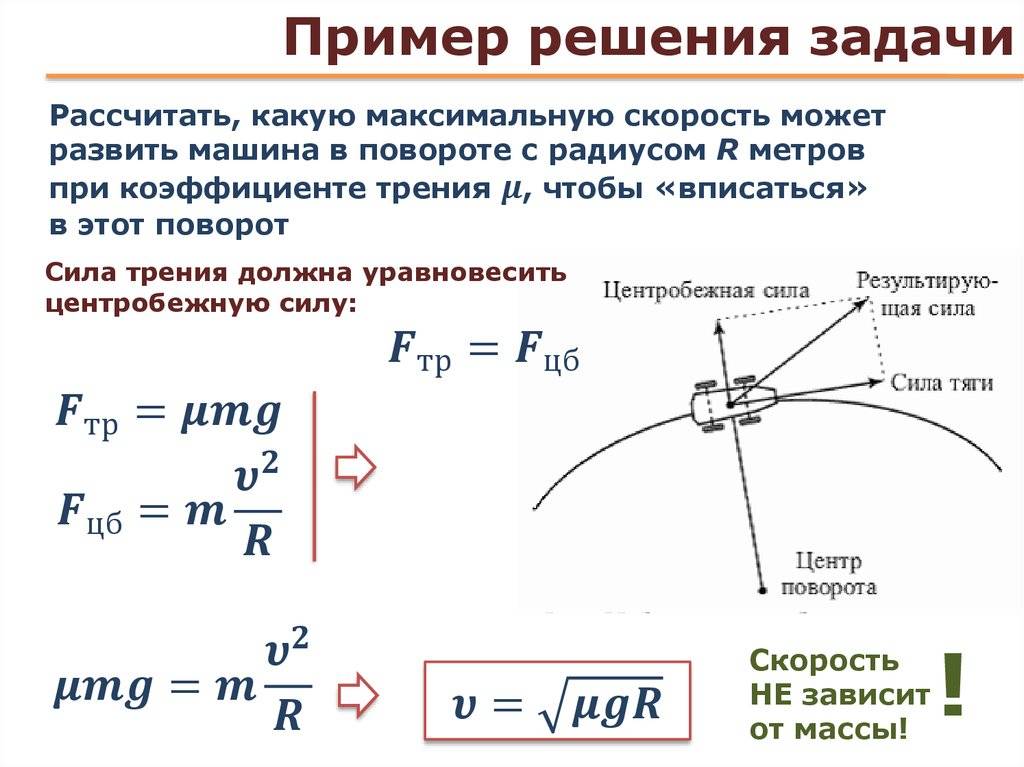
Практическое применение центростремительной силы

Классическим примером центростремительной силы является предмет, висящий на веревке. Здесь натяжение веревки создает центростремительную силу «притяжения».

Центростремительная сила является «толкающей» силой в случае со стеной смерти мотоциклиста.

Центростремительная сила используется для лабораторных центрифуг. Здесь частицы, взвешенные в жидкости, отделяются от нее с помощью ускоряющих трубок, которые ориентированы таким образом, что более тяжелые частицы (т.е. объекты с большей массой) притягиваются ко дну трубок. Хотя центрифуги обычно отделяют твердые вещества от жидкостей, они также могут отделять жидкости, например, образцы крови, или отдельные компоненты газов.

Газовые центрифуги используются для отделения более тяжелого изотопа урана-238 от более легкого изотопа урана-235. Более тяжелый изотоп извлекается из вращающегося цилиндра. Более тяжелая фракция отбирается и подается в другую центрифугу. Процесс повторяется до тех пор, пока газ не будет достаточно обогащен.

Телескоп с жидким зеркалом (LMT) может быть построен путем вращения отражающего жидкого металла, например, ртути. Поверхность зеркала имеет форму параболоида, потому что центростремительная сила зависит от квадрата скорости. Поэтому высота вращающегося жидкого металла пропорциональна квадрату его расстояния от центра. Интересную форму, которую принимает вращающаяся жидкость, можно наблюдать, вращая ведро с водой с постоянной скоростью.

Центробежная сила – это чувство

Когда автомобиль резко поворачивает налево, пассажиры могут чувствовать себя «брошенными» вправо от машины. Или в нижней части петли на американских горках гонщики могут почувствовать себя прижатыми к своим сиденьям.

Эти чувства – результат инерция; тем не мение, нет сила (хотя ее можно назвать кажущаяся сила). Инерция описывает тенденцию объекта сопротивляться изменениям в его движении, как описано в Первом законе Ньютона, Законе инерции.

Когда машина резко поворачивает или американские горки падают, человеческие тела внутри уже движутся с некоторой скоростью в определенном направлении. Согласно Закону инерции эти тела изначально сопротивляться изменяя их скорости.

Пассажиры все еще движутся вперед в пространстве, когда машина резко начинает уезжать влево – так что вместо того, чтобы быть “брошенным вправо”, машина на самом деле врезаясь в них слева, когда он внезапно движется. Как только их тела догоняют и начинают двигаться влево, ощущение грохота заканчивается.

Точно так же и на американских горках тела все еще движутся вниз, когда горки начинают толкать их вверх. Пока их тела не догонят, чтобы соответствовать новой скорости каботажного судна, они чувствуют, что их бросают на внешнюю сторону тележек. Их тела все еще движутся к тележкам, поскольку тележки теперь движутся к их телам.

Примеры центробежной силы

Здесь мы рассмотрим пример, в котором применим принципы центробежной силы.

Шарик, прикрепленный к концу струны, вращается по кругу с угловой скоростью $286\;\text{degrees}/\text{sec}$. Если длина струны равна $60\;\mathrm{cm}$, то какова центробежная сила, действующая на шарик?

Шаг 1: Запишите заданные величины

$$\mathrm m=100\mathrm g,\;\mathrm\omega=286\;\deg/\sec,\;\mathrm r=60\mathrm{cm}$$$.

Шаг 2: Преобразование единиц измерения

Преобразование градусов в радианы. $$\text{Radians}=\text{Deg}\;\times\;\pi/180\;$$ $$=286\;\times\pi/180\;$$ $$=5\;\text{radians}$$.

Следовательно, $286\;\text{degrees}/\text{sec}$ будет равно $5\;\text{radians}/\text{sec}$.

Пересчет сантиметров в метры $$1\;\mathrm{cm}\;=\;0.01\;\mathrm{m}$$$ $$60\;\mathrm{cm}\;=\;0.6\;\mathrm{m}$$.

Шаг 3: Рассчитайте центробежную силу, используя угловую скорость и радиус

Используя уравнение $$F\;=\;\frac{mV^2}r\;=\;m\;\omega^2\;r$$ $$\mathrm F\;=100\;\mathrm g\times5^2\;\mathrm{rad}^2/\sec^2\times0.6\;\mathrm m$$ $$F\;=\;125\;\mathrm N$$$

На шар действует центробежная сила, равная $125\;\mathrm N$ На это можно посмотреть и с другой стороны. Центростремительная сила, необходимая для поддержания кругового движения шара с указанными выше характеристиками, равна $125\;\mathrm N$.

Что такое центробежная сила

Сначала примеры:

Когда стиральная машинка отжимает мокрое бельё, барабан быстро крутится. Так вода выходит из ткани.
Метание молота на олимпийских играх. Перед броском спортсмен кружится вокруг своей оси, а потом отпускает молот.
В китайских цирках популярен номер с мотоциклистами в металлическом шаре. Каскадёров запускают внутрь конструкции, где они разгоняются и ездят по всей поверхности шара. Даже по верху.
На крутом повороте пассажиров внутри автомобиля заносит в сторону.

Центробежная сила (F_цб) — это сила, которая действует на криволинейно движущееся тело с угловой скоростью. Чтобы её найти, используют две формулы: F = ma или F= mv2/r, где m — масса, a — ускорение, v — скорость r — радиус.

F_цб возникает при инерции, когда тело перемещается криволинейно. Она зависит от двух вещей: центра вращения; радиуса до предмета. Например, метание молота: спортсмен начинает кружиться вокруг своей оси вместе со снарядом. Металлическая проволока натягивается шаром, который весит как школьный портфель. Когда атлет отпускает ручку, молот улетает по прямой.

Молот натягивает проволоку, когда кружится в воздухе. На него действует инерция, которая “вырывают” его с траектории движения. Вместе с ними шар удерживают атлет и натянутая проволока. Поэтому, снаряд не улетит, пока спортсмен не отпустит ручку.

Теперь обратно к формуле: радиус — длина проволоки; масса — вес шара; скорость — это насколько быстро атлет кружится; центр вращение — сам спортсмен.