Введение
Математика является фундаментом для любой современной научной дисциплины. И ни для кого не секрет, что почти все методы современной науки о данных (включая машинное обучение) строятся на тех или иных математических вычислениях.
Порой, будучи специалистом по обработке и анализу данных (или даже junior-аналитиком ) необходимо знать базовую математику, чтобы правильно применять ее методы. Для других целей можно использовать API или уже готовый алгоритм.
Но, в то же время, владение хорошими знаниями по математике, на которой строится ваш алгоритм для создания рекомендации по использованию продукта, никогда не навредит. Это даст вам преимущество перед вашими конкурентами и поможет вам сохранить уверенность в своих знаниях. Всегда полезно знать, что находится под капотом, а не просто сидеть за рулем, ничего не зная о машине.
Конечно, вам понадобятся и другие знания, навыки программирования, немного деловой хватки, уникальное аналитическое мышление и любознательность, касающиеся данных, которые так необходимы для ведущего специалисте по обработке и анализу данных. В данной статье я попытался собрать самые важные математические понятия, чтобы помочь вам в этом начинании.
Примечания[]
- Номенклатура специальностей научных работников. Утверждена Приказом Министерства науки и технологий Российской Федерации от 25 января 2000 г. № 17/4
- Государственный образовательный стандарт высшего профессионального образования. Специальность 01.01.00. «Математика». Квалификация — Математик. Москва, 2000 (Составлено под руководством О. Б. Лупанова)
| Эта статья или раздел описывает ситуацию применительно лишь к одному региону (Россия), возможно, нарушая при этом правило о взвешенности изложения.Вы можете помочь Науке, добавив информацию для других стран и регионов. |
Для улучшения этой статьи желательно?:
|
| Выделить Разделы математики и найти в:
|
|
|
- Страница – краткая статья
- Страница 1 – энциклопедическая статья
- Разное – на страницах: 2 , 3 , 4 , 5
- Прошу вносить вашу информацию в «Разделы математики 1», чтобы сохранить ее
Ассоциированные математические науки
Прикладная математика во многом пересекается со статистикой.
Прикладная математика связана со следующими математическими науками:
Научные вычисления
Научные вычисления включают прикладную математику (особенно численный анализ ), информатику (особенно высокопроизводительные вычисления ) и математическое моделирование в научной дисциплине.
Исследование операций и наука об управлении
Исследования операций и наука об управлении часто преподаются на факультетах инженерии, бизнеса и государственной политики.
Статистика
Прикладная математика во многом пересекается со статистикой. Статистические теоретики изучают и улучшают статистические процедуры с помощью математики, а статистические исследования часто поднимают математические вопросы. Статистическая теория опирается на теорию вероятностей и решений и широко использует научные вычисления, анализ и оптимизацию ; для планирования экспериментов статистики используют алгебру и комбинаторный дизайн . Прикладные математики и статистики часто работают на факультетах математических наук (особенно в колледжах и небольших университетах).
Актуарная наука
Актуарная наука применяет вероятность, статистику и экономическую теорию для оценки рисков в страховании, финансах и других отраслях и профессиях.
Математическая экономика
Математическая экономика – это применение математических методов для представления теорий и анализа проблем экономики. Применяемые методы обычно относятся к нетривиальным математическим методам или подходам. Математическая экономика основана на статистике, вероятности, математическом программировании (а также других вычислительных методах ), исследовании операций, теории игр и некоторых методах математического анализа. В этом отношении она напоминает финансовую математику (но отличается от нее) , другую часть прикладной математики.
Согласно классификации предметов математики (MSC), математическая экономика попадает в классификацию категории 91:
- Теория игр, экономика, социальные и поведенческие науки
Применимая математика
Применимая математика – это раздел прикладной математики, хотя нет единого мнения относительно точного определения. Иногда термин «применимая математика» используется, чтобы провести различие между традиционной прикладной математикой, которая развивалась вместе с физикой, и многими областями математики, которые сегодня применимы к реальным проблемам.
Математики часто проводят различие между «прикладной математикой», с одной стороны, и «приложениями математики» или «прикладной математикой» как внутри, так и за пределами науки и техники, с другой. Некоторые математики подчеркивают термин «применимая математика» для отделения или разграничения традиционных прикладных областей от новых приложений, возникающих из областей, которые ранее считались чистой математикой. Например, с этой точки зрения эколог или географ, использующий модели населения и применяющий известную математику, будет заниматься не прикладной, а скорее прикладной математикой. Даже такие области, как теория чисел, которые являются частью чистой математики, теперь важны в приложениях (таких как криптография ), хотя они, как правило, не считаются частью области прикладной математики как таковой . Такие описания могут привести к тому, что применимая математика будет рассматриваться как совокупность математических методов, таких как реальный анализ , линейная алгебра , математическое моделирование , оптимизация , комбинаторика , вероятность и статистика , которые полезны в областях, выходящих за рамки традиционной математики и не относящихся к математической физике .
Другие авторы предпочитают описывать прикладную математику как объединение «новых» математических приложений с традиционными областями прикладной математики. Таким образом, при таком взгляде термины прикладная математика и прикладная математика взаимозаменяемы.
Прочие дисциплины
Граница между прикладной математикой и конкретными областями применения часто размыта. Многие университеты преподают математические и статистические курсы за пределами соответствующих факультетов, на факультетах и в областях, включая бизнес, инженерию , физику , химию , психологию , биологию , информатику , научные вычисления и математическую физику .
Алгебра, арифметика, математика: в чем разница?
Арифметика
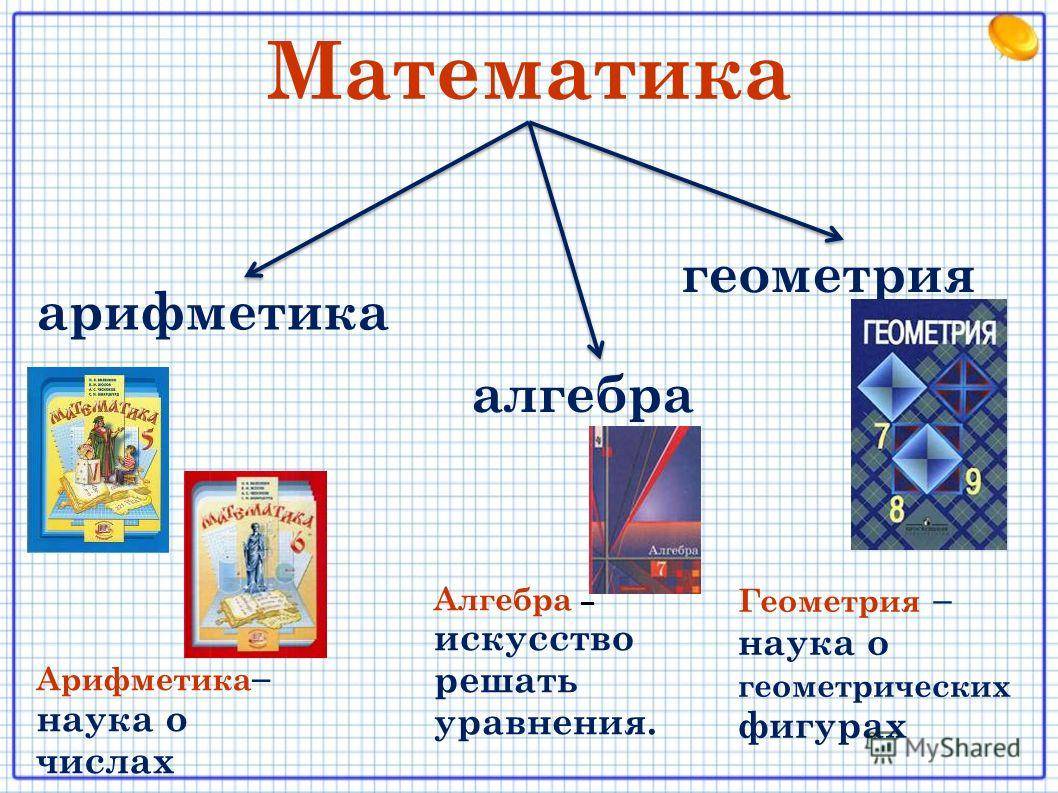
Арифметика — это раздел математики, который изучает основные операции с числами, такие как сложение, вычитание, умножение и деление. В рамках арифметики изучаются также свойства чисел, системы счисления и решение уравнений. Она является базовым знанием и применяется в повседневной жизни для решения простых задач и подсчета.
Алгебра
Алгебра — это раздел математики, который изучает символические и числовые выражения и их свойства. Она включает в себя работу с переменными, алгебраическими операциями, алгебраическими уравнениями и неравенствами. Алгебра используется для решения сложных вычислений, моделирования математических отношений и развития абстрактного мышления.
Математика
Математика — это широкий исследовательский предмет, который включает в себя различные разделы, включая арифметику, алгебру, геометрию, теорию вероятности и другие. Математика изучает структуру, формулирует и проверяет законы и свойства чисел и объектов. Она имеет множество применений в науке, технологии, экономике и других областях исследования.
- Арифметика — основные операции с числами
- Алгебра — символические и числовые выражения
- Математика — широкий предмет, включающий различные разделы
Таким образом, алгебра, арифметика и математика являются взаимосвязанными и важными разделами математики, каждый из которых имеет свои уникальные аспекты изучения чисел и их свойств.
Чем математика отличается от других наук?
Математика — очень сложная для постижения наука. Наверное, с ней может сравниться только физика, и то она все же уступает. Погружение в какую-либо науку я бы сравнил с такой ситуацией: ты поднимаешься по лестнице, открываешь дверь и выходишь на этаж с множеством других дверей. Это стандартный путь изучения любой дисциплины: ты устал, пока поднимался, но на финише ты собой доволен. Даже можешь открыть много смежных дверей в другие науки и все поймешь.
Изучение математики — это когда ты долго поднимаешься по лестнице, хочешь выйти на этаж и понимаешь, что вместо открытого пространства там стены, а на них еще более крутые лестницы, по которым нужно карабкаться. Ты лезешь дальше, с огромным трудом достигаешь следующего этажа и думаешь, что здесь-то ты уже можешь говорить на одном языке с великими учеными — с Пуанкаре, Перельманом, но вокруг опять только стены и лестница. И так этаж за этажом. У тебя нет никакого раздолья, нет награды за твои труды. Что ты получаешь за свое стремление вверх? Пропуск к еще большим трудам. Вот так устроена математика. За это мы ее обожаем. Потому что она никогда не дает расслабляться.
История
Численное решение уравнения теплопроводности на модели корпуса насоса с использованием метода конечных элементов .
Исторически прикладная математика состояла в основном из прикладного анализа , в первую очередь из дифференциальных уравнений ; теория приближений (в широком смысле слова, включая представления , асимптотические методы, вариационные методы и численный анализ ); и прикладная вероятность . Эти области математики имели прямое отношение к развитию ньютоновской физики , и на самом деле различие между математиками и физиками не проводилось четко до середины XIX века. Эта история оставила педагогическое наследие в Соединенных Штатах: до начала 20 века такие предметы, как классическая механика, часто преподавались на факультетах прикладной математики в американских университетах, а не на факультетах физики , а механика жидкости все еще может преподаваться на факультетах прикладной математики. Кафедры инженерии и информатики традиционно использовали прикладную математику.
Почему математика, а не арифметика?
Для того чтобы понять, чем отличается курс арифметики от математики, показать разницу между тем, как учили арифметике раньше и как изучают математику сейчас, вспомним свои школьные годы.
Целостность знания разбивалась на отдельные части — сложение, вычитание, деление, умножение, и каждая часть усваивалась отдельно. В первом классе элементы знания подавались как отдельные единицы, а во втором классе и в третьем эти умения и навыки соединялись в целостное знание. Только после того, как первоклассники усваивали каждое математическое действие в отдельности, они начинали складывать их в единое целое, приступая к изучению математических отношений и связей.
Теперь в младших классах используется более содержательный метод обучения математике. В новой программе предусматривается обучение детей одновременно сложению и вычитанию, умножению и делению.
Новый школьный курс математики объединяет арифметику с элементами геометрии и алгебры. Дети уже с первого класса узнают, как взаимосвязаны математические действия. Это более содержательный путь обучения, и он дает больше, чем простая сумма знаний о сложении, вычитании, делении и умножении.
Усвоение математических знаний становится более емким и приводит к пониманию сути математических действий. Например, вот какие преобразования можно произвести с простым примером: 1 + 2 = 3, но и 2 + 1 = 3.
Значит, уже в первом классе школьники узнают переместительный закон сложения: от перемены мест слагаемых сумма не изменяется. С этими же числами можно произвести вычитание: 3-2=1. И закончит целостную единицу математического знания решение примера: 3-1 = 2.
Усвоение школьниками этих четырех примеров помогает им разобраться во взаимосвязи математических отношений.
Где пригодится высшая математика
Для тех, кто не знал, сообщаем: все современные достижения науки и техники — заслуга высшей математики. Без сложных математических вычислений не было бы возможно создание таких технологий, как:
- программное обеспечение;
- Wi-Fi;
- Google, Yandex;
- компьютерные игры;
- мобильные приложения;
- цифровые фотографии;
- компьютеры;
- смартфоны и многое другое.
Изучение и разведка космоса, создание ракет и космических кораблей, запуск и функционирование спутников — все это заслуга математики.
Тесно связаны с математикой молекулярная биология и медицина. Многие открытия в области генной инженерии стали возможны благодаря математическим вычислениям и алгоритмам. Создание большинства медицинских приборов было бы невозможно без математических знаний.
Методы и подходы в исследованиях
В математике и алгебре используются различные методы и подходы для проведения исследований и решения математических задач. Вот несколько основных методов и подходов, используемых в этих областях:
Дедуктивный метод — это метод рассуждения, основанный на логических заключениях из общих утверждений к конкретным случаям. При использовании дедуктивного метода, математики формулируют аксиомы и определения, и затем выводят теоремы и результаты на основе этих начальных предположений.
Индуктивный метод — это метод рассуждения, основанный на наблюдениях и обобщениях. Используя индуктивный подход, математики проводят серию экспериментов или анализируют большой объем данных, чтобы выявить общие закономерности и сделать обобщения.
Аналитический метод позволяет разбить исследуемую задачу на более простые составляющие и анализировать их по отдельности. В математике и алгебре аналитический метод часто используется для изучения функций и уравнений. Математики анализируют свойства и графики функций, применяют различные методы дифференцирования и интегрирования для получения более подробной информации о функциях.
Компьютерное моделирование стало незаменимым инструментом в математике и алгебре. С помощью компьютерных программ и алгоритмов математики могут проводить сложные вычисления, строить графики, визуализировать данные и анализировать математические модели. Компьютерное моделирование позволяет исследователям провести больше экспериментов и получить результаты, которые трудно получить вручную.
Это лишь некоторые из методов и подходов, используемых в исследованиях в математике и алгебре. Многие проблемы и задачи требуют использования комбинации различных методов и подходов для получения наиболее полной и точной информации.
Чистые математики
«Чистая математика» – это широкий термин для области математиков, которые изучают теоретические конструкции в математике. Чистая математика в основном преследует цель открыть новое понимание самой математики, необязательно для решения проблем в реальном мире. Основным понятием чистой математики является общность. Чистые математики стремятся обобщить математические понятия, чтобы применить их к широкому кругу различных разделов математики. Области изучения включают такие отрасли, как функциональный анализ, теория чисел, абстрактная алгебра, геометрия и реальный анализ.
Обучение специальности
Получить образование в области прикладной математики — значит, иметь хороший шанс найти высокооплачиваемую работу. Согласно ОКСО (Общероссийский классификатор специальностей по образованию), эта область науки готовит специалистов инженерного и компьютерного направлений.
Процесс поступления
Многие выпускники школ стремятся поступить в вузы с математическим уклоном. Такой вариант позволит рассчитывать на качественную и всестороннюю подготовку, а также возможность дальнейшего трудоустройства по специальности.
Поступать на «Прикладную математику» лучше всего сразу после окончания обучения в школе (желательно в физмате). Благодаря этому можно будет быстрее подготовиться и лучше написать ЕГЭ. В большинстве высших учебных заведений придётся сдавать 3−4 экзамена. Первый из них будет профильным, а второй и все последующие — произвольными (по выбору ВУЗа).
Наиболее частые экзамены:
- русский язык;
- математика;
- ИКТ (информатика и информационно-коммуникационные технологии);
- физика;
- иностранный язык.
Изучаемые дисциплины
Согласно госстандарту в образовательной сфере, прикладная математика занимается изучением десятков базовых и профильных предметов. Некоторые из них предусматривают дистанционное обучение, которое позволяет быстрее освоить большие объёмы информации.
Базовые предметы:
- политология;
- история;
- основы экологии;
- информатика;
- экономика;
- социология;
- алгебра и геометрия;
- физика;
- иностранный язык;
- введение в математический анализ.
В число основных профильных предметов входят:
- все разделы математики;
- языки и методы программирования;
- теоретическая механика;
- операционные системы;
- информатика и компьютерные сети;
- все разделы физики;
- психология и педагогика.
Приобретаемые знания и навыки
Обучение специальности длится 4 года. После получения степени бакалавра у студента есть шанс поступить в магистратуру, где придётся учиться ещё 1 год. За все 5 курсов молодые специалисты приобретают бесценные знания и навыки, которые им понадобятся после окончания ВУЗа. В их число входят:
- применение новых технологий на практике;
- создание сложных алгоритмов;
- работа с различным ПО;
- умение читать программы, написанные популярными языками программирования;
- создание разнообразных математических моделей;
- знание базовых исследовательских методов;
- применение современного программного обеспечения для выполнения поставленной задачи;
- понимание всех нововведений в математике;
- глубокие познания во всех областях физики;
- умение применять методы аналитической геометрии и линейной алгебры.
Лучшие вузы
В России насчитывается более 100 учебных заведений, где можно пройти обучение по специальности «Прикладная математика». Большинство из них находится в региональных и областных центрах.
Лучшие вузы страны:
- Белгородский государственный национальный исследовательский институт;
- Тверской государственный университет;
- Нижегородский государственный технический университет;
- Томский политехнический институт;
- Якутский государственный университет;
- Национальный исследовательский университет «Высшая школа экономики».
FAQ – 💬
Какие виды математики существуют?
Математика как учебная дисциплина подразделяется в Российской Федерации на элементарную математику, изучаемую в средней школе и образованную дисциплинами: арифметика элементарная алгебра элементарная геометрия: планиметрия и стереометрия
Как называется высшая математика?
Высшая математика — курс обучения в средних и высших учебных заведениях, включающий высшую алгебру и математический анализ.
Какой самый сложный раздел математики?
Топология. Доводилось достаточно длительно время наблюдать студентов математического факультета некоторого локального университета. Самый сложный предмет был для них топология.
В чем разница между математикой и прикладной математикой?
По ироническому утверждению В. И. Арнольда, разница между чистой и прикладной математикой не научная, а социальная и заключается в том, что чистому математику платят за открытие математических фактов, в то время как прикладному математику платят за решение практических задач.
Как называется человек который не знает математику?
Как правило, дискалькулия — врожденное расстройство. Обычно у ребенка с таким диагнозом кто-то из родителей тоже плохо понимает математику. Но бывает и так, что в семье экономистов и физиков-ядерщиков рождаются дети, не способные к арифметике.
Где востребованы математики?
Но если рядовому гражданину достаточно элементарных основ этой науки, то для успешной работы в некоторых сферах человеческой деятельности требуются глубокие знания данной дисциплины.
- Математик …
- Экономист …
- Бухгалтер …
- Финансист …
- Налоговый инспектор …
- Программист …
- Архитектор …
- Инженер
Где нет математики?
Можно поступить в колледж и изучить психологию, биохимию, фармацевтику, ветеринарию. Тем более не обязательно разбираться в математических нюансах выпускникам с творческими талантами….Остановимся подробнее на профессиях без профильной математики.
- Лингвистика. …
- Юриспруденция. …
- Ресторанный сервис. …
- Педагогика. …
- Медицина.
Что сложнее сдать физику или математику?
Сложнее всего поверить, что физика — это просто. Многие школьники боятся физики как огня — а на самом деле физика гораздо легче, скажем, курса математики. В физике легко проводить параллели и аналогии с реальной жизнью. Большинство законов интуитивно понятнее, чем сложные доказательства и теоремы в математике.
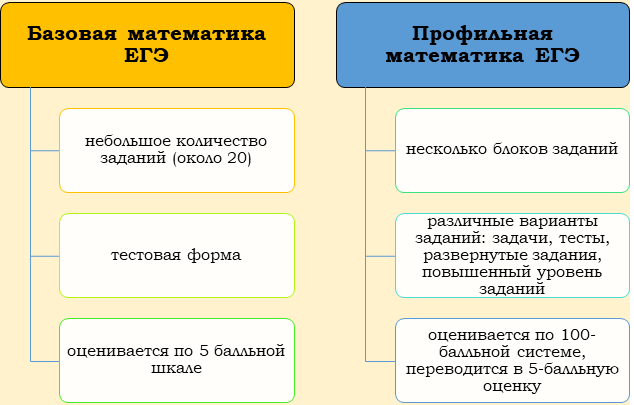
Почему с базовой математикой нельзя поступить в вуз?
Базовая математика используется только для аттестата об образовании. Для получения документа достаточно перейти порог. Результат выставляется по пятибалльной шкале, поэтому вузы он не интересует и при поступлении не суммируется с баллами за другие предметы.
Какой тип мышления у математиков?
Определение математического мышления таково: математическое мышление – это абстрактное теоретическое мышление, объекты которого лишены вещественности, но при этом они могут быть интерпретированы любым произвольным образом с одним лишь условием – должны сохраняться заданные между объектами отношения.
Куда не надо сдавать математику?
Можно поступить в колледж и изучить психологию, биохимию, фармацевтику, ветеринарию. Тем более не обязательно разбираться в математических нюансах выпускникам с творческими талантами….Остановимся подробнее на профессиях без профильной математики.
- Лингвистика. …
- Юриспруденция. …
- Ресторанный сервис. …
- Педагогика. …
- Медицина.
Что относится к математике?
Одно из первых определений предмета математики дал Декарт : К области математики относятся только те науки, в которых рассматривается либо порядок, либо мера, и совершенно не существенно, будут ли это числа, фигуры, звёзды, звуки или что-нибудь другое, в чём отыскивается эта мера.
Что такое сущность математики?
Сущность математики… представляется теперь как учение об отношениях между объектами, о которых ничего не известно, кроме описывающих их некоторых свойств, — именно тех, которые в качестве аксиом положены в основание теории… Математика есть набор абстрактных форм — математических структур.
Кто такой знаменитый математик?
«Знаменитым математиком» обычно называет героя своих детских стихов и книг — академика Иванова — автор Эдуард Успенский. В 1986 году по книге режиссёром Владимиром Поповым на студии Союзмультфильм был снят мультфильм.
Что означает слово математика?
Слово «математика» произошло от др.-греч. μάθημα, что означает «изучение, знание, наука», и др.-греч. μαθηματικός, первоначально означающего «восприимчивый, успевающий» , позднее — «относящийся к изучению», впоследствии ставшее «относящийся к математике».
Какими знаниями и качествами должен обладать математик?
Итак, мы уже разобрались, что математику необходимо высшее образование и особый склад ума, чтобы его получить. Однако и сам процесс изучения математики заметно улучшает когнитивные и прочие способности человека. Какими же качествами должен обладать математик, чтобы в итоге состояться как специалисту?
Основные качества математика:
- Аналитические способности.
- Логическое мышление.
- Абстрактное мышление.
- Отличная память.
- Умственная работоспособность.
- Способность к концентрации внимания.
- Умение находить нестандартные решения.
- Личная организованность.
- Целеустремленность.
О целеустремленности хотелось бы сказать подробнее
Ввиду большого разнообразия потенциальных сфер приложения усилий математика, важно еще на этапе обучения определиться, какое именно направление привлекает больше всего, чем именно хотелось бы заниматься в будущем, и уже со 2-3 курса получать необходимые дополнительные знания и навыки. Ни один вуз не дает в руки профессию «один к одному»
Всегда будут поправки на эксклюзивные требования работодателя и конкретные условия работы.
Поэтому следует заранее изучить потенциально интересные сферы деятельности, а в идеале начать сотрудничать с конкретными компаниями еще на этапе учебы. Это может быть подработка или стажировка, а некоторые работодатели даже берутся организовать производственную практику для студентов. Чтобы пройти весь путь от идеи до высокооплачиваемого специалиста, конечно же, нужна целеустремленность.
Что же касается конкретных знаний, получаемых в вузе, то учебные программы по специальности «математика» во всех вузах страны достаточно сходны. Могут быть незначительные вариации, когда какой-либо предмет где-то начинают изучать на втором курсе, а где-то на третьем, или к концу первого курса в каком-то вузе по предмету сдают зачет, а в каком-то экзамен. Это в большей степени имеет значение для студентов, решивших перевестись из вуза в вуз и сдающих академразницу.
В целом же всем будущим математикам предстоит фундаментальная подготовка и изучение таких предметов как математический анализ, теория чисел, дифференциальные уравнения, функциональный анализ, теоретическая механика и прочие.
Далее, в зависимости от специализации, начинают преподавать аналитическую теорию чисел, компьютерную алгебру, теорию полей, криптологию, асимптотическое интегрирование нелинейных дифференциальных уравнений и другие увлекательные предметы. Для примера можно изучить учебные планы МГУ им. Ломоносова по математическим специальностям .
Как мы уже говорили выше, вуз не дает полного пакета знаний, необходимых для работы, и математику в любом случае придется что-то дополнительно осваивать самостоятельно, как и любому другому специалисту. Эффективно организовать данный процесс и учиться действительно тому, что нужно, научит наша программа «Лучшие техники самообразования».
В любом случае люди, имеющие математическое образование, выгодно отличаются от гуманитариев и экономистов тем, что имеют определенный тип мышления, позволяющий унифицировать практически любые расчеты и минимизировать затраты ресурсов на производство расчетной части. То, что без расчетов в современном мире не обходится ни одна отрасль, думается уже понятно.
Полезность
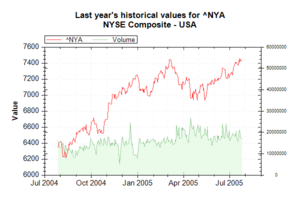
Математические финансы связаны с моделированием финансовых рынков.
Исторически, математика была наиболее важной в естественных науках и технике. Однако после Второй мировой войны вне физических наук возникли новые области математики, такие как теория игр и теория социального выбора, которые выросли из экономических задач.. С появлением компьютера появились новые приложения: изучение и использование самой новой компьютерной технологии (информатика) для изучения проблем, возникающих в других областях науки (вычислительная наука), а также математика вычислений (например, теоретическая информатика, компьютерная алгебра, численный анализ)
Статистика, вероятно, является наиболее распространённой математической наукой, используемой в социальных науках, но и другие области математики, особенно экономическая, становятся всё более полезными в этих дисциплинах.
С появлением компьютера появились новые приложения: изучение и использование самой новой компьютерной технологии (информатика) для изучения проблем, возникающих в других областях науки (вычислительная наука), а также математика вычислений (например, теоретическая информатика, компьютерная алгебра, численный анализ). Статистика, вероятно, является наиболее распространённой математической наукой, используемой в социальных науках, но и другие области математики, особенно экономическая, становятся всё более полезными в этих дисциплинах.
Что произойдет в математической сфере в ближайшие годы?
Математический прогноз на ближайшие 5–10 лет дать невозможно: наши горизонты планирования — это тысячи лет. Поэтому десятилетие тут играет незначительную роль. За это время можно успеть подкрутить какие-то гипотезы, начать что-то проверять. В чистой математике бывают прорывы — скажем, с 1975 по 2005 годы были сняты чуть ли не пять величайших математических загадок, включая Последнюю Теорему Ферма и гипотезу Пуанкаре. А вот в технической сфере ничего существенного не изобретали уже давно. Сейчас, по сути, допиливаются идеи, которые были высказаны в 50–60-е годы.
Мне кажется, технический прогресс приостановился. Сейчас он связан с интернетом, банковскими картами, шифрованием, кодированием — но все это тоже вещи не быстрые, не на ближайшие пять лет.
Чем отличается математика от прикладной математики
Математика – это фундаментальная наука, которая занимается изучением разных структур, их отношений и порядков. Математика, как наука, появилась очень давно, наверное, с возникновением человечества. Уже в раннем палеолите люди были знакомы с основами счета. У людей всегда была необходимость что-то подсчитать или пересчитать. Известно, что для счета люди пользовались и пальцами, и камнями, и палками и различными метками. Историю развития математики отсчитывают именно с того момента, как люди научились считать.
Для того чтобы понять, чем отличается прикладная математика от математики, нужно рассмотреть основные понятия, которыми оперирует одна и вторая наука.
Математика
Если посмотреть определение математики в различных словарях и энциклопедиях, то можно заметить, что единого точного определения математики не существует. Однако мы все интуитивно понимаем, что такое математика. Наилучшее определение было дано, наверное, Бурбаки.
Бурбаки – это псевдоним группы математиков, которые написали серию книг по математике. По определению Бурбаки, математика изучает отношения между какими-то объектами. Каждый объект описывается с точки зрения его количественных характеристик. Сущностью математики является описание некоторого набора абстрактных структур.
Из этого определения становится понятно, чем занимается теоретическая математика. Она должна описать отношения различных структур данных.
Математика делится на элементарную и высшую части. Элементарную математику изучают в школе.
Она включает в себя такие разделы, как:
- Арифметика.
- Начала алгебры.
- Геометрия.

Высшая математика состоит из:
- Математического анализа.
- Алгебры.
- Аналитической геометрии.
- Дифференциальных уравнений.
- Теории вероятности.
- Математической статистики.
- Теории чисел.
- Функционального анализа.
В теоретической математике разработан математический аппарат, основу которого составляют обозначения, аксиомы, утверждения. А на базе уже этого аппарата развивается дальнейшая теория, доказываются теоремы и выводятся определенные правила.
Прикладная математика
Прикладная математика является частью математики. Если говорить обычным языком, прикладная математика – это математика, которая используется на практике. Прикладная математика изучает и разрабатывает способы применения теоретической математики в других дисциплинах. Если вернуться к словам математика Харди, то в отличие от чистой математики, прикладная математика приносит практическую пользу.

Разделы прикладной математики
- Численные методы.
- Математическая физика.
- Программирование.
- Оптимизация вычислений.
- Теория игр.
- Криптография.
- Теория оптимального управления.
- Биоматематика.
- Биоинформатика и др.
Предметом исследования прикладной математики является применение теоретических математических методов чистой математики в других науках. Например, строятся экономические модели и с помощью методов теории оптимального управления вырабатываются наилучшие управленческие решения.

В физике или химии для проведения каких-либо экспериментов или опытов, не всегда представляется возможным провести испытания на реальном объекте. Поэтому строится его модель. Модель – это уменьшенная или увеличенная копия реального объекта, которая имеет точно такие же свойства.
Криптография – это наука, которая занимается шифрованием. В шифровании используются различные математические методы и алгоритмы.
Таким образом, из вышеприведенного понятно, что и чистая математика, и прикладная математика использует одни и те же методы. Но чистая математика использует эти методы для дальнейшего развития теории, а прикладная математика использует математические методы и теорию чистой математики для того, чтобы можно было решать реальные задачи в физике, химии, биологии, статистике, экономике и в других науках.
Получение новых знаний и открытий
Одна из основных задач высшей математики — разработка новых методов и концепций, которые позволяют решать сложные проблемы и расширять границы математического знания. Во время изучения высшей математики студенты учатся анализировать математические модели и проблемы на более глубоком уровне, а также применять различные методы и техники для их решения.
Исследования в области высшей математики могут привести к открытию новых теорем, формулированию и доказательству математических закономерностей и законов, которые могут найти применение в других научных дисциплинах и технологиях. Например, основы высшей математики лежат в основе современных наук о данных, искусственного интеллекта, криптографии, физики высоких энергий и других областей.
Кроме того, высшая математика способствует развитию воображения, логического мышления и абстрактного мышления студентов. Она помогает студентам учиться видеть связи и закономерности, которые неочевидны на первый взгляд, и формулировать сложные проблемы на математическом языке.
В целом, изучение высшей математики не только приближает нас к пониманию сложных фундаментальных проблем, но и помогает нам получать новые знания и открытия, которые могут изменить нашу жизнь и научить нас смотреть на мир с новой перспективы.
Зарплата и карьерный рост
Прежде чем начинать обучение, нужно узнать, какую зарплату получают молодые специалисты и опытные сотрудники. Она зависит не только от опыта, но и от квалификации, места работы, набора личных качеств.
Квалифицированный специалист имеет шанс построить прекрасную карьеру. На начальной её стадии сотрудник продолжает обучение, только делает это не в ВУЗе, а на рабочем месте. Набравшись опыта, он может быть допущен к выполнению самостоятельной работы. Дальнейший прогресс может привести к получению руководящей должности в какой-либо компании или места в одной из иностранных фирм.
https://youtube.com/watch?v=Q7GmwXFY0yE