Чем отличается круг от окружности — основные сведения

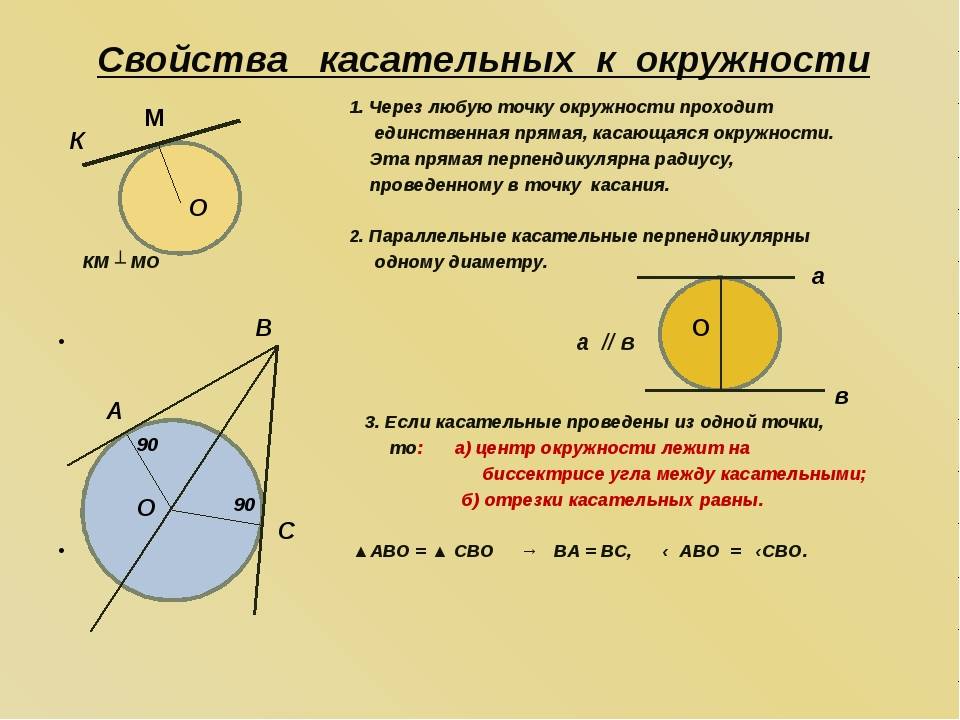
Применение в реальной жизни

В инженерии и архитектуре круг и окружность широко применяются при проектировании и строительстве различных конструкций. Например, при проектировании мостов и тоннелей окружности используются для определения радиусов изгибов дорожных поверхностей, а круги — для создания круглых площадок и амфитеатров.

В науке круги и окружности применяются в геодезии и при изучении движения тел. Для измерения углов использование окружностей и кругов является общепринятой практикой. Кроме того, в астрологии круги используются при построении астрологических гороскопов и карт рождения.

В искусстве круги и окружности часто используются как символы и элементы дизайна. Окружности могут быть использованы для создания абстрактных композиций и геометрических узоров, а круги — для выделения точек акцента и создания гармоничного баланса визуальных композиций.

Таким образом, круги и окружности являются универсальными геометрическими фигурами, которые не только помогают нам понять законы природы, но и позволяют применять их в различных сферах нашей повседневной жизни.

Взаимное отношение хорд и их расстояний от центров

В математике существует тесная связь между хордами и расстояниями от их центров до окружности. Основные вопросы связаны с изучением углов и зависимостей между ними.

В прямоугольном четырехугольнике с хордами, проходящими через центр окружности, мера углов, образованных этими хордами, совпадает с половиной угла вписанного в окружность четырехугольника. Так, если угол вписанного четырехугольника равен 90 градусов, то и угол, образованный хордами, будет равен 45 градусам.

Расстояние от центра окружности до хорды является отношением двух дуг, ограниченных хордой. Это отношение всегда меньше, чем 1. Также, существует зависимость между этим относительным расстоянием и диаметром окружности: чем больше диаметр, тем меньше отношение.

Взаимное отношение расстояний от центров окружности и круга, описанного вокруг нее, также имеет свои характеристики и сходство с отношением расстояний до хорд. Все эти свойства могут быть объяснены с помощью теории углов и практической пользы в построении и измерении в математике.

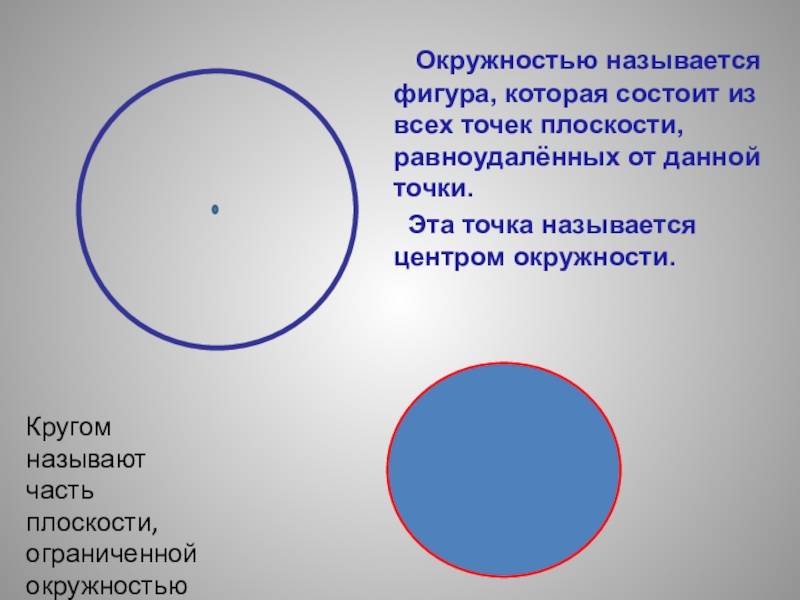
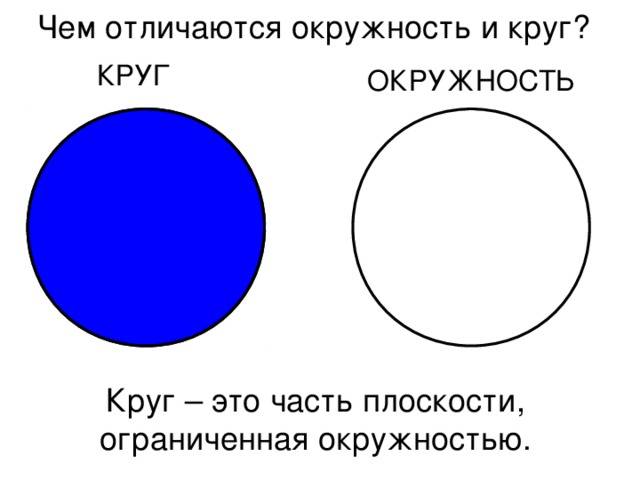
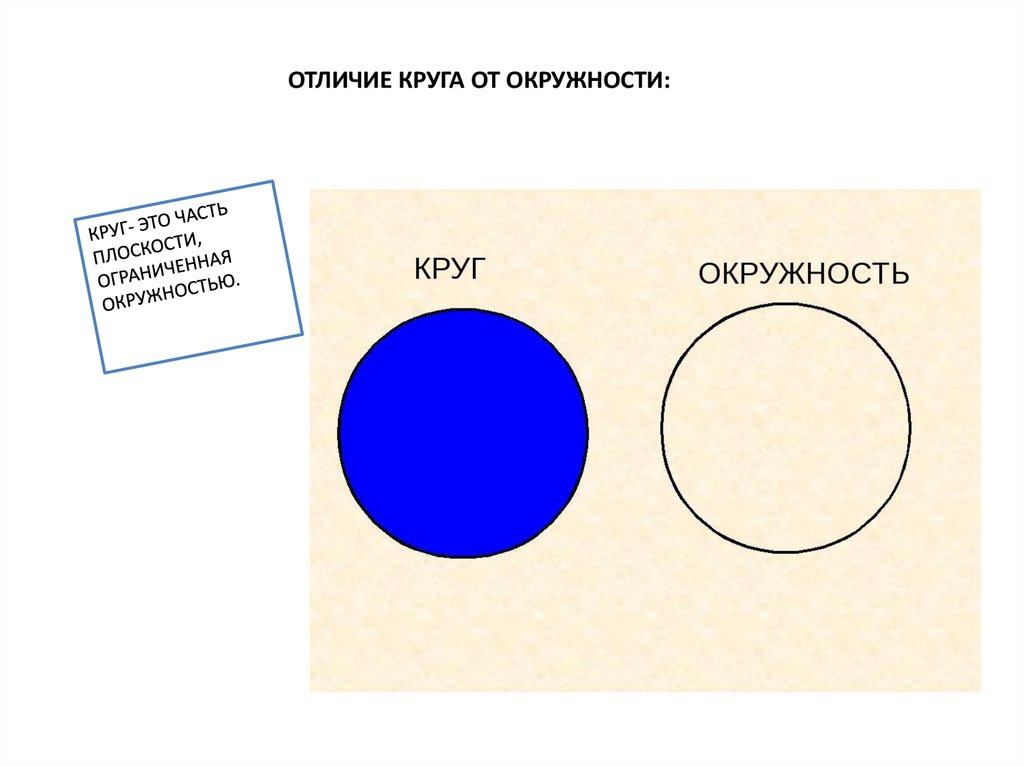
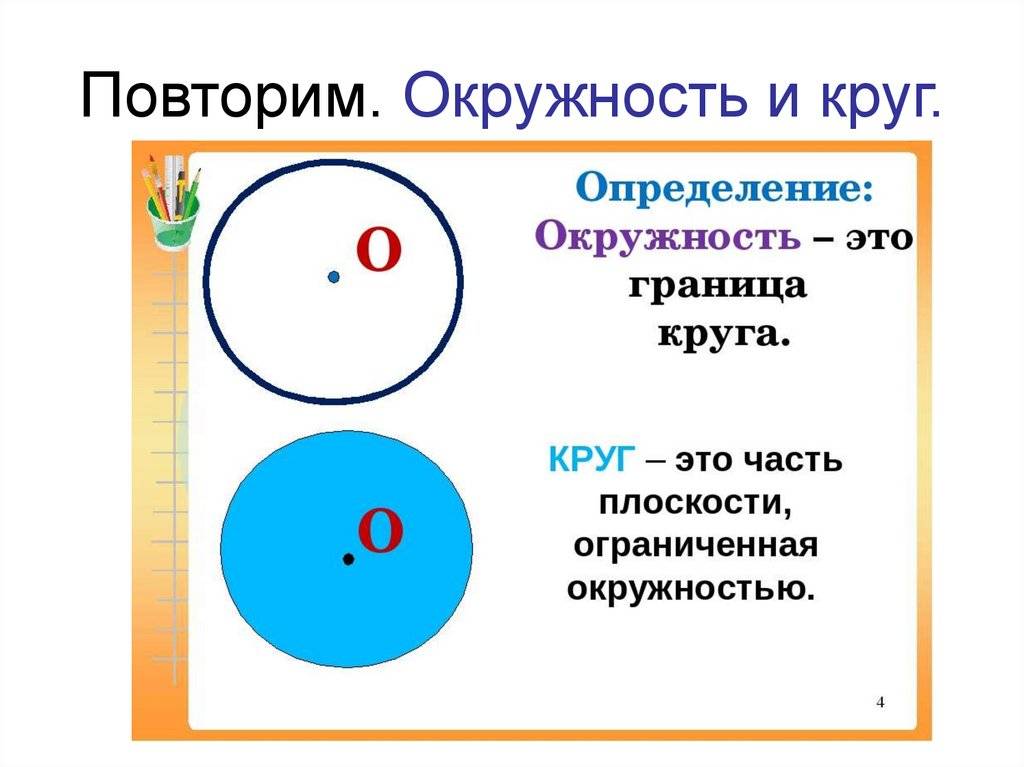
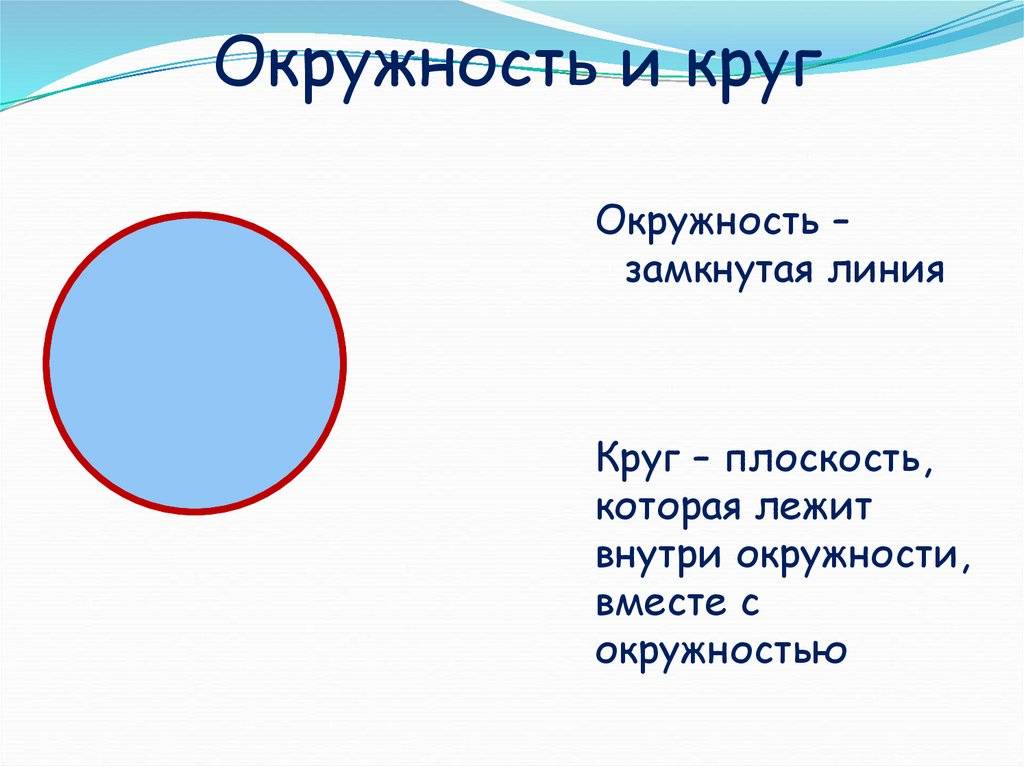
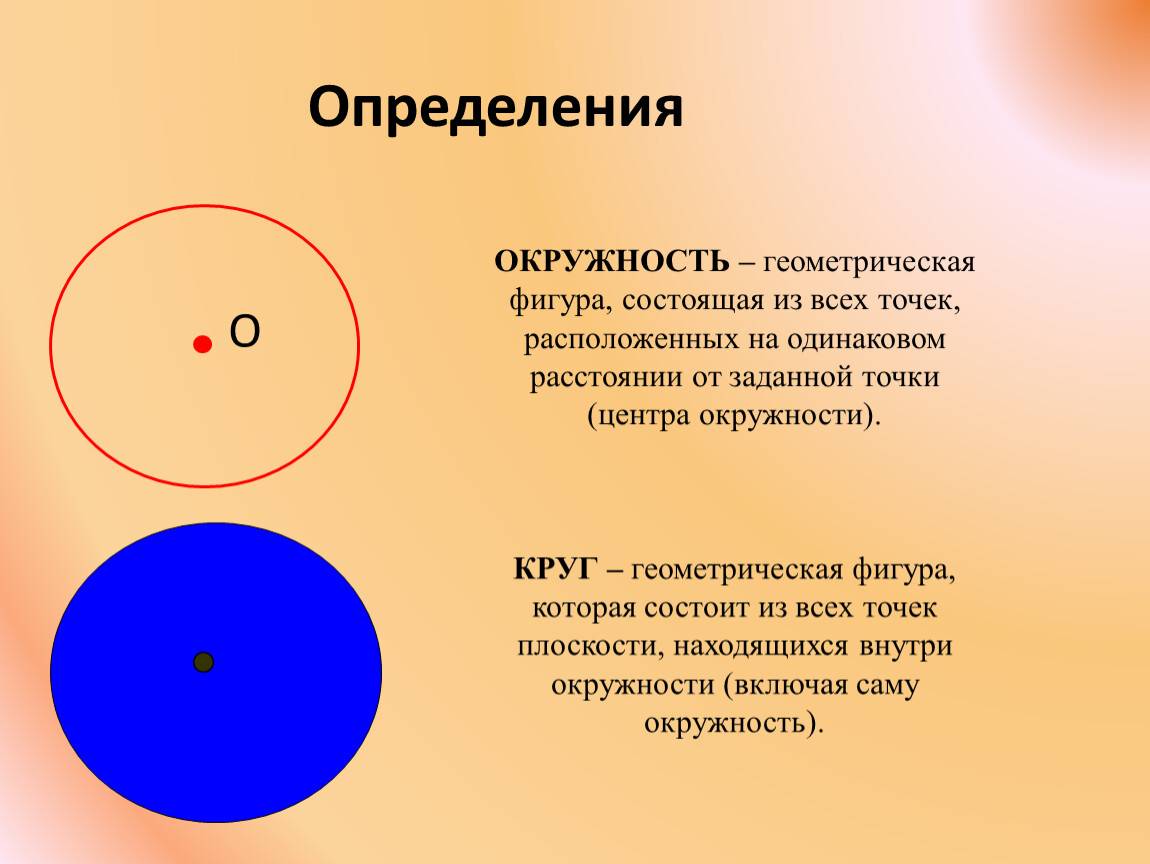
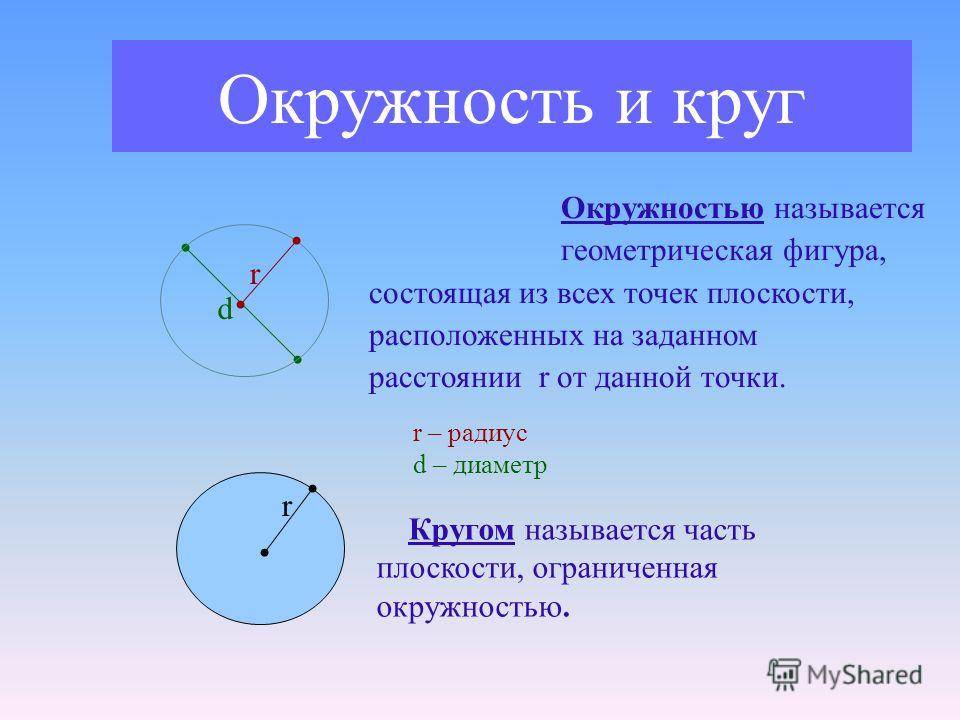
Окружность и круг — это два различных понятия. Окружность это геометрическая фигура, состоящая из всех точек равноудаленных от одной точки, называемой центром окружности. Круг, в свою очередь, это область, ограниченная окружностью.

Как построить окружность?

Окружность можно построить с помощью циркуля и линейки. Нужно выбрать центр окружности, определить радиус или диаметр, и провести соответствующую дугу или хорду.

Изучение хорд и их расстояний от центров окружности является важной частью математической теории окружностей и кругов. Это новые знания, которые позволяют лучше понять свойства и особенности окружностей и кругов и применить их на практике

Длина окружности

Рассмотрим – угольникnправильный     B1B2…Bn , вписанный в окружность радиуса радиуса R, и опустим из центра O окружности перпендикуляры на все стороны многоугольника (рис. 2).

Рис.2

Поскольку – угольникаnплощадь   B1B2…Bn   равна

то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R:

C = 2πR.

Следствие. Длина окружности радиуса 1 равна   2π.

Как найти длину окружности через диаметр

Диаметр — отрезок, который соединяет две точки окружности и проходит через её центр. Формула длины окружности через диаметр:

l=πd, где

π— число пи — математическая константа, равная 3,14

d — диаметр окружности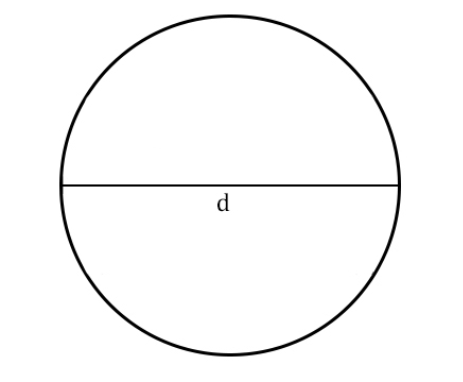

Как найти длину окружности через радиус

Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:

l=2πr , где

π — число пи, равное 3,14

r — радиус окружности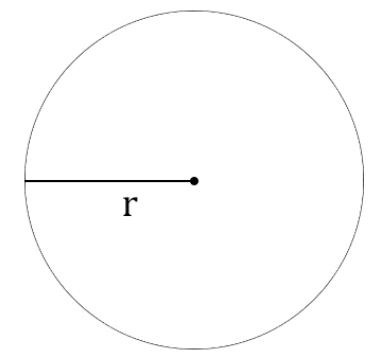

Как вычислить длину окружности через площадь круга

Если вам известна площадь круга, вы также можете узнать длину окружности:

где:

• π — число пи, равное 3,14
• S — площадь круга

Как найти длину окружности через диагональ вписанного прямоугольника

Как измерить окружность, если в нее вписан прямоугольник: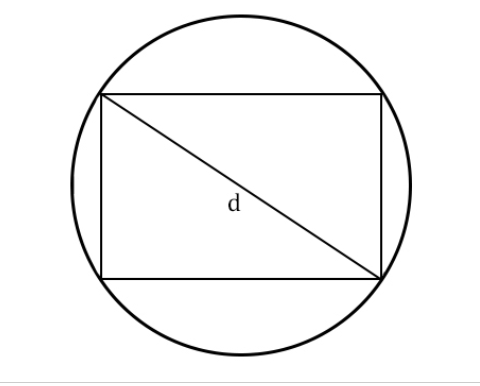

l=πd, где

• π — число пи, равное 3,14
• d — диагональ прямоугольника

Как вычислить длину окружности через сторону описанного квадрата

Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата: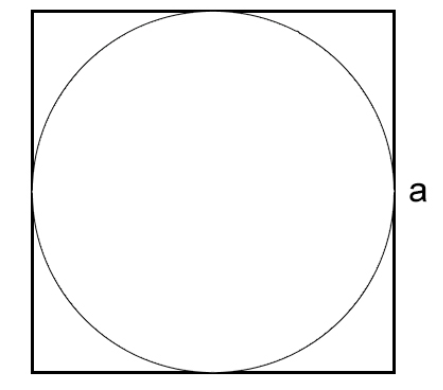

l=πa, где

• π — математическая константа, равная 3,14
• a — сторона квадрата

Как найти длину окружности через стороны и площадь вписанного треугольника

Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:

где:

• π — математическая константа, она всегда равна 3,14
• a — первая сторона треугольника
• b — вторая сторона треугольника
• c — третья сторона треугольника
• S — площадь треугольника

Как найти длину окружности через площадь и полупериметр описанного треугольника

Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.

где:

• π — математическая константа, равная 3,14
• S — площадь треугольника
• p — полупериметр треугольника

Как вычислить длину окружности через сторону вписанного правильного многоугольника

Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:

где:

• π — математическая константа, равная 3,14
• a — сторона многоугольника
• N — количество сторон многоугольника

Окружность

Циркуль — инструмент для черчения окружностей и дуг, также может быть использован для измерения расстояний.

окружность

Если установить ножку циркуля с иглой в какую-либо точку, а ножку с грифелем повернуть вокруг этой точки, у нас получится замкнутая линия. Она называется окружностью.

{"questions":[{"content":"На каких рисунках присутствуют окружности? Выберите все подходящие ответы:`img_choice-1`","widgets":{"img_choice-1":{"type":"img_choice","options":[["https://obrazavr.ru/wp-content/uploads/2023/05/nozhniczy-2.svg"],["https://obrazavr.ru/wp-content/uploads/2023/05/skrepki.svg"],["https://obrazavr.ru/wp-content/uploads/2022/07/keys.svg"],["https://obrazavr.ru/wp-content/uploads/2022/07/bicycle.svg"]],"answer":}}}]}

ImGist определил, что разница между кругом и окружностью заключается в следующем:

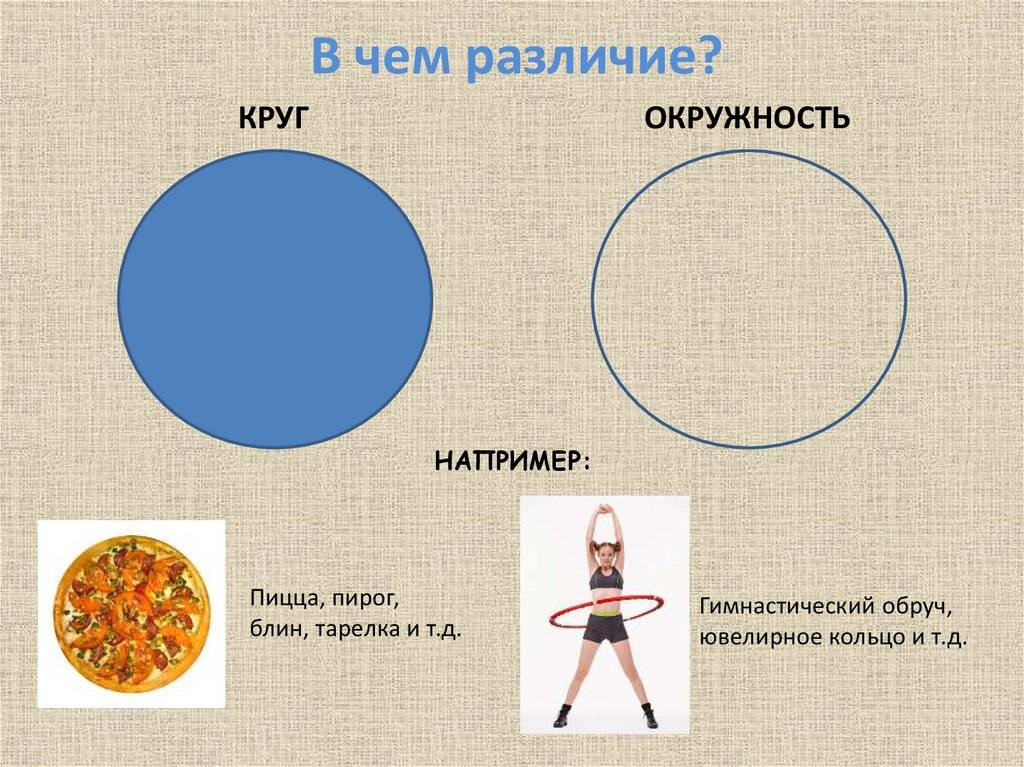
Окружность является лишь частью круга, его границей, в то время как круг является более обширной и полноценной фигурой;
Окружность – это кривая линия, состоящая из бесчисленного множества точек, равноудаленных от центра, а круг представляет собой не только сумму этих точек окружности, но также и все те точки, которые расположены внутри этой самой окружности.

Окружность
– это огромное количество точек на плоскости, равноудаленных от некой точки этой же плоскости, именуемой центром окружности. Окружность представляет собой замкнутую кривую, лежащую от центра на фиксированном расстоянии, нарываемом радиусом окружности.

Круг
– это огромное количество точек плоскости, удаленных от некой точки этой же плоскости, именуемой центром круга, на расстояние, не превышающеей определенной величины, именуемой радиусом круга. Круг представляет собой сплошную фигуру, включающую окружность и все точки, лежащие в ней.

Следовательно, круг – это участок плоскости, а окружность – черта этого участка. Потому есть возможность говорить о площади круга и длине окружности, однако неправильно говорить о длине круга и площади окружности.

Так как точки окружности удалены от центра на расстояние, не превышающее радиуса, то они все принадлежат кругу. Другими словами, окружность принадлежит кругу, который она ограничивает. В особых случаях может рассматриваться круг в отсутствие границы – огромное количество точек круга, не принадлежащих его границе (окружности).

Окружность разделяет плоскость на две части – лежащую снутри и лежащую снаружи. Попрасть из одной части в другую нереально в отсутствие скрещения окружности. Площаль внутренней части конечна, площадь наружной части нескончаема.

Центр окружности не принадлежит окружности (кроме вырожденного варианта окружности нулевого радиуса). Центр круга всегда принадлежит кругу, т.к. находится снутри ограничивающей его окружности.

openclass.ru – методическая разработка «Окружность и круг»
otvet.mail.ru – чем отличается круг от окружности?

NMitra
В Opera есть баг: у вложенного элемента углы не закругляются. Это можно подправить, дописав

#ball:after {content: “”;position: absolute;top: 0; bottom: 0; right: 0; left: 0;box-shadow: 0 0 0 100px #fff;border-radius: 100%; }

Но тогда тень в Гугл Хром “обрезанная” получается. Поскольку Опера переезжает на движок Google, то я сделала выбор в пользу его браузера.
Космо Мизраил
Прикольно.Сейчас делаю дизайн как раз с планетами, но аватарки и другие изображения приходится делать плоскими, потому что img не применишь box-shadow: inset.
NMitra
Сделайте фоном background. Скоро благодаря поддержки трансформации CSS можно будет добавлять объём. Предвестники http://codepen.io/html5web/pen/pnbwo
Космо Мизраил
Мдо, вроде-бы для вебкита, а не работает х) Это будет вступать лет пять ещё, до этого надо ещё дожить

Фоны сделать не всегда получится, а вот наложить поверх изображения элемент с заданными стилями очень даже можно. Но это если известны размеры изображения.Пример: http://jsfiddle.net/9qzm6/

Ещё нашёл скрипт, который выполняет эту работу самостоятельно:http://www.htmldrive.net/items/demo/1156/Multiple-CSS3-Image-StylesЗдесь он сам определяет размер, если изображение загрузилось. Нужен jQuery.

Это так, на заметку
NMitra
Там нужны настройки какие-то устанавливать.. Это сильно вперёд:))

Пжалст я ваш постоянный читатель уже год как минимум
Анонимный
IE 11Все анимировано))
NMitra
Молодцом IE, дотянулось. Осталась Хрому убрать -webkit-, он теперь в числе отстающих.

Применение в практике

Разница между кругом и окружностью имеет свое применение в различных областях практики:

• Геометрия: окружность используется для измерения длины окружности, площади круга и других геометрических параметров. Круг, в свою очередь, широко применяется при решении задач о нахождении площади фигуры, описываемой кругом.
• Инженерия: круг и окружность используются при проектировании и изготовлении колес, шестерен, зубчатых колес, цилиндрических труб и других деталей, имеющих круглую форму.
• Физика: в физике окружность помогает определить расстояние, которое прошел объект по окружности, а также углы поворота и ускорение.
• Архитектура: круговая форма часто используется в архитектуре для создания куполов, качелей, фонтанов и других элементов, добавляющих эстетическую привлекательность зданию или ландшафту.
• Компьютерная графика: окружности и круги активно применяются в создании графических объектов, таких как шары, колеса, кнопки и многое другое.

Таким образом, понимание разницы между кругом и окружностью помогает не только в теоретических вычислениях, но и в практическом применении в различных областях науки, инженерии и искусства.

Основные определения и свойства

Фигура	Рисунок	Определения и свойства
Окружность		Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Дуга		Часть окружности, расположенная между двумя точками окружности
Круг		Конечная часть плоскости, ограниченная окружностью
Сектор		Часть круга, ограниченная двумя радиусами
Сегмент		Часть круга, ограниченная хордой
Правильный многоугольник		Выпуклый многоугольник, у которого все стороны равны и все углы равны
	Около любого правильного многоугольника можно описать окружность

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Дуга

Часть окружности, расположенная между двумя точками окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Сектор

Часть круга, ограниченная двумя радиусами

Сегмент

Часть круга, ограниченная хордой

Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны Около любого правильного многоугольника можно описать окружность

•       Определение 1. Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
•       Определение 2. Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.

Замечание 1. Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.

      Определение 3. Числом π (пи) называют число, равное площади круга радиуса 1.

Замечание 2. Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.

Окружность и круг

Круг — это замкнутая плоская кривая, состоящая из всех точек плоскости, равноудаленных от определенной точки. Эта точка называется центром окружности. Линия, соединяющая центр и точки на окружности, называется радиусом. Длина линии также называется радиусом.

Окружность — это часть плоскости, которая лежит внутри окружности. Другими словами, это совокупность точек на плоскости, расстояние которых от определенной точки, называемой центром окружности, не превышает определенного неотрицательного числа. Номер. Это называется радиусом круга.

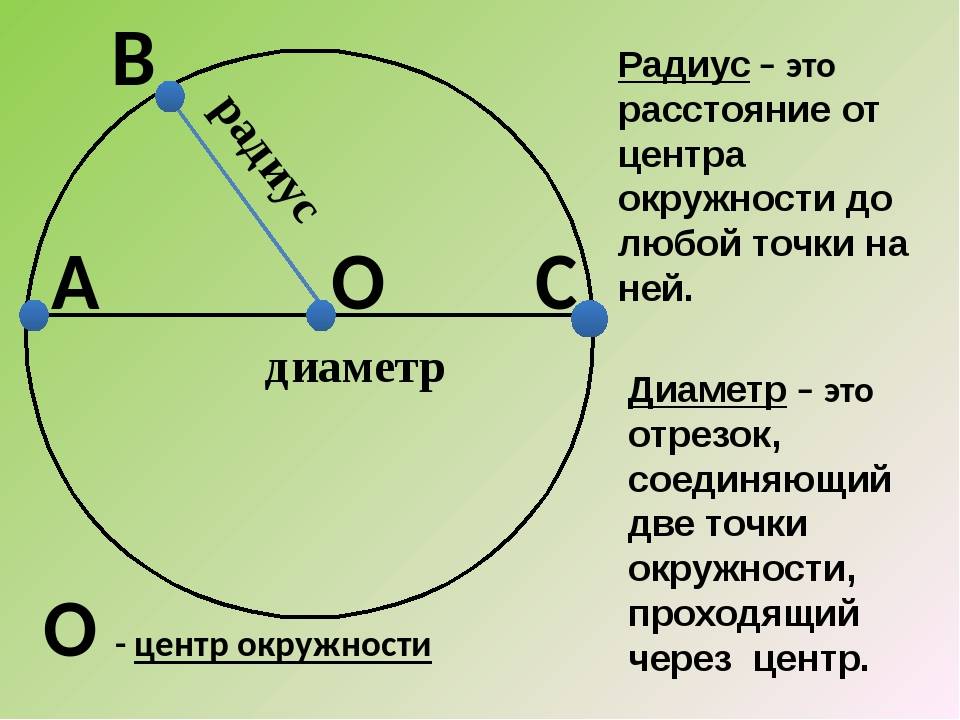
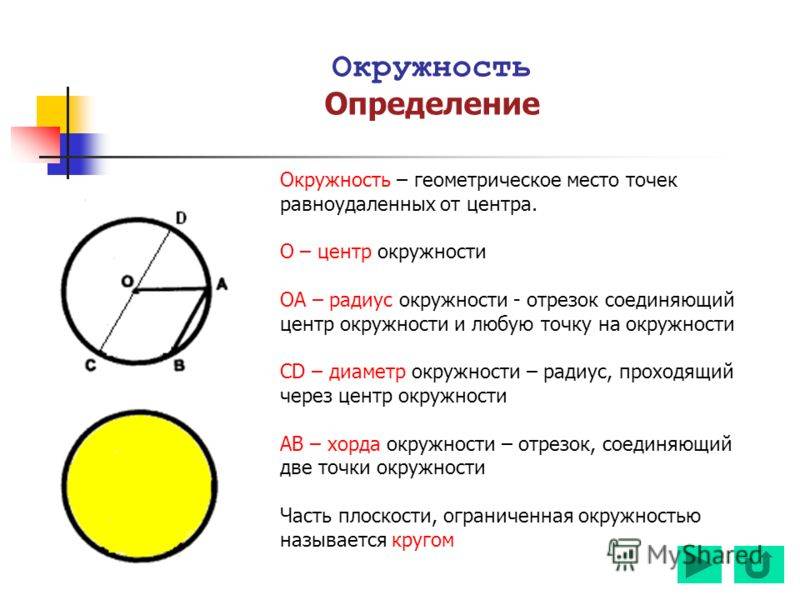
Определение окружности и круга

Значение. Круг — это фигура, состоящая из всех точек плоскости на определенном расстоянии от определенной точки.

Эта точка называется центром окружности. Расстояние точки от центра окружности называется радиусом окружности. Радиусом также называется часть окружности, соединяющая точку и ее центр.

Значение. Часть окружности, соединяющая две точки, называется струной. Нить, проходящая через центр, называется диаметром.

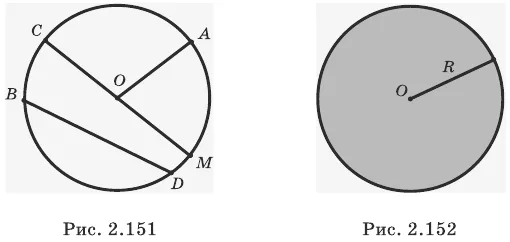
На рисунке 2.151 изображена окружность с центром в точке O. Отрезок OA — радиус окружности, BD — строка окружности, а CM — диаметр окружности.

Значение. Окружность — это фигура, состоящая из всех точек плоскости на расстоянии, меньшем или равном одной конкретной точке.

Эта точка называется центром окружности, а это расстояние — радиусом окружности. Граница окружности — это окружность, центр и радиус которой совпадают (рис. 2.152).

Пример:

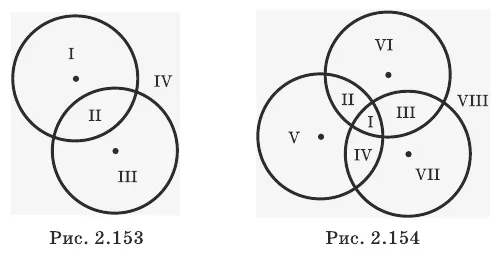
Какое максимальное количество различных отрезков, не имеющих ничего общего, кроме своих границ, может разделить уровень на a) две окружности и b) три окружности?

Используйте эту диаграмму, чтобы показать соответствующий случай согласования. Запишите ответы: а) четыре сегмента (рис. 2.153) — б) восемь сегментов (рис. 2.154).

Центральные углы и дуги окружности

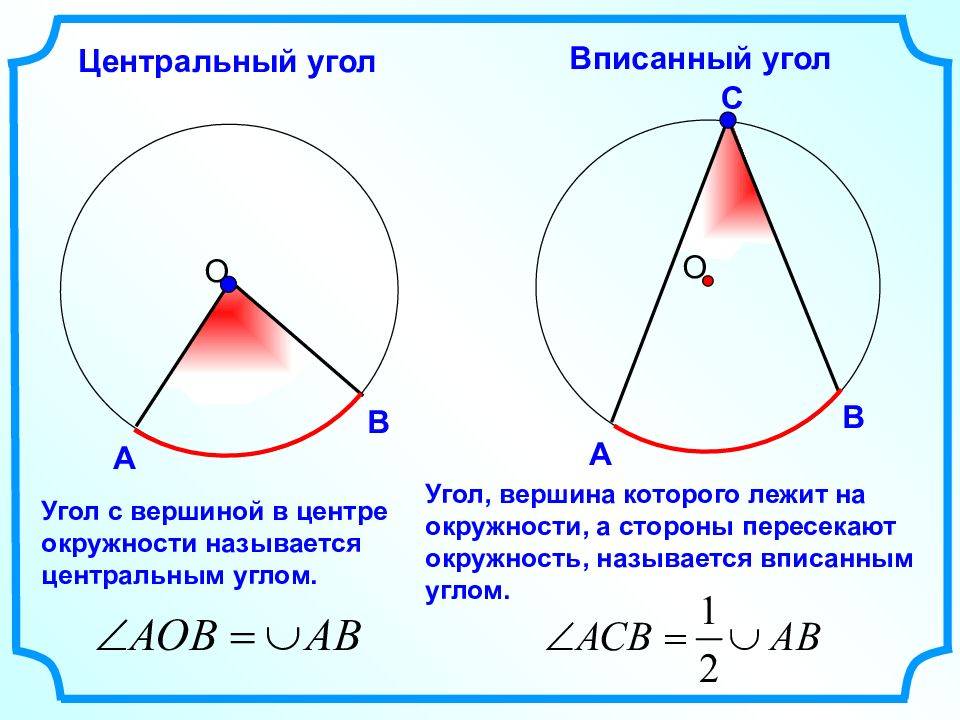
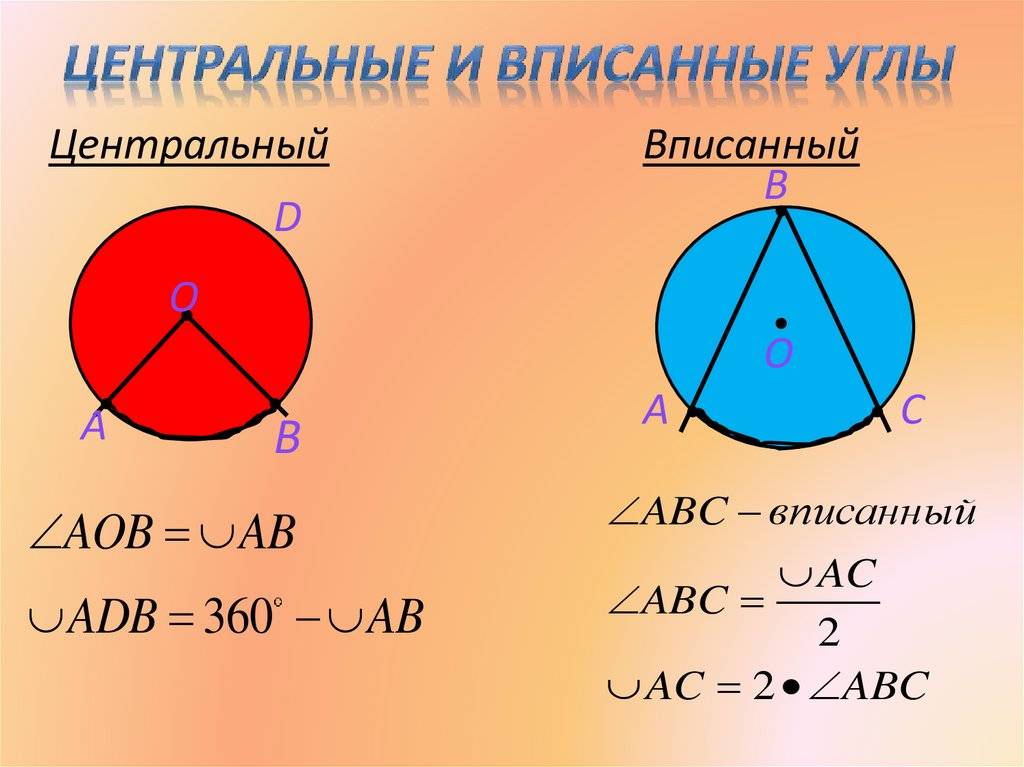
Предположим, что вершина угла совпадает с центром окружности (рис. 2.155). Угол AOB называется центральным углом.

Определение. Центральный угол окружности — это плоский угол с центром в вершине.

Внутренняя круговая часть угла называется дугой окружности, соответствующей этому центральному углу.

Значение. Пересечение окружности и ее центрального угла называется дугой окружности.

Мера градуса дуги окружности равна мере градуса соответствующего центрального угла.

Градусная мера дуги АВ на рисунке 2.155 равна градусной мере угла АОВ. Градусная мера дуги АВ обозначается

Можно ввести еще одну важную единицу дуги. При измерении углового значения дуги окружности единицей измерения является угловое значение этой дуги окружности, длина которой равна радиусу окружности. Эта единица измерения размера угловой дуги называется радиусом.

Сформулируем некоторые свойства измерения дуги окружности.

-Измеренный порядок дуги не зависит от размера окружности.

-Соответствующие дуги двух концентрических окружностей на рис. 2.156 имеют одинаковый порядок (размер).

-По мере увеличения размера дуги (в пределах определенной окружности) ее мера также увеличивается.

Окружности (или круги) равны, если у них равные радиусы. Мы можем говорить о равных дугах, но равная дуга может быть либо одной окружностью, либо равной окружностью.

Значение. Две дуги одинаковых или равных окружностей называются равными, если они имеют одинаковую степень меры.

Применение круга в математике и геометрии

Круг используется во множестве различных задач и концепций. Некоторые из его применений включают:

1. Вычисления площади и длины окружности: Площадь круга вычисляется по формуле S = πr², где π (пи) — это математическая константа, равная примерно 3,14159, а r — радиус круга. Длина окружности вычисляется по формуле L = 2πr. Эти вычисления могут быть полезными для решения проблем, связанных с областями, периметрами и длинами кривых.
2. Геометрическая оптика и астрономия: Круг используется в оптике для описания линз и зеркал, а также для вычисления пути света через линзы и преломление света. В астрономии он используется для описания орбит планет и других небесных тел.
3. Статистика: Круг используется в статистике для построения круговых диаграмм и отображения данных в виде секторов, пропорциональных их относительным значениям. Это позволяет наглядно представить информацию и сравнить ее части.
4. Механика и инженерия: Круг используется для моделирования и анализа движения колес, шестеренок и других круглых механизмов. Он также применяется в анализе сил и равновесия, формулировании уравнений движения и проектировании эффективных конструкций.
5. Музыка и искусство: Круг используется в музыке для измерения углов между нотами и строительства музыкальных гамм. В искусстве он может быть использован для построения и симметрии композиций, а также для создания эффектов перспективы и глубины.

Это лишь некоторые примеры применения круга в математике и геометрии, и его использование может быть намного более обширным и разнообразным

Знание основных свойств и способов работы с кругом является важной частью математической и геометрической подготовки и помогает понять и анализировать различные аспекты окружающего мира

Круг

Начертим на плоскости окружность, разделив ее тем самым на две части.Внутренняя часть, ограниченная пределами окружности, называется кругом.

Это как если бы мы взяли большой лист бумаги, нарисовали на нем кружок и вырезали его ножницами:

Круг также состоит из множества точек, и все они лежат на нашей маленькой плоскости. Расстояние от этих точек до центра круга не превышает радиус.

{"questions":[{"content":"Выберите рисунки, в изображении которых присутствует круг:`img_choice-1`","widgets":{"img_choice-1":{"type":"img_choice","options":[["https://obrazavr.ru/wp-content/uploads/2022/03/kartochka4.svg"],["https://obrazavr.ru/wp-content/uploads/2022/11/rascheska-greben-zerkalo.svg"],["https://obrazavr.ru/wp-content/uploads/2022/07/pillow.svg"],["https://obrazavr.ru/wp-content/uploads/2022/01/night-morning.svg"]],"answer":}}}]}

Геометрические примеры окружности и круга

Окружность — это множество точек на плоскости, расположенных на одном и том же расстоянии от центра. Окружность имеет форму замкнутой кривой, которая не имеет ни начала, ни конца. Она может быть задана с помощью радиуса и координат центра или с помощью уравнения.

Круг, с другой стороны, это область плоскости, ограниченная окружностью. Круг имеет два важных элемента — окружность и плоскость. Окружность является границей круга, в то время как плоскость — это множество всех точек внутри окружности и на ней.

Другими словами, окружность это только граница, а круг — это окружность с добавлением всех точек внутри нее.

Примеры геометрических фигур, которые могут быть окружностями и кругами, включают:

Фигура	Описание
Колесо	Колесо автомобиля или велосипеда представляет собой окружность, так как все его точки находятся на одинаковом расстоянии от центра.
Столовая тарелка	Столовая тарелка имеет форму круга, так как она ограничена окружностью и все ее точки находятся внутри окружности.
Фрисби	Фрисби также имеет форму круга, так как он ограничен окружностью и все его точки находятся внутри окружности.
Монета	Монета имеет то же свойство, что и фрисби — она ограничена окружностью и все ее точки находятся внутри окружности.

Это лишь некоторые примеры применения окружностей и кругов в геометрии. Они часто используются для моделирования форм и объектов в реальном мире, а также для решения различных задач в математике.

Примеры окружности в ежедневной жизни

Круг — понятие, тесно связанное с окружностью. Как и окружность, круг имеет форму окружности, но также содержит внутреннюю часть, заполненную полностью. Например, кружочки на наших утюгах и столовых тарелка подобного формата.

Окружность и круг также используются в архитектуре и дизайне. Многие здания и сооружения имеют форму окружности или круга. Некоторые здания даже имеют круглую планировку, что создает эффект симметрии и гармонии.

Другой пример использования окружностей можно найти в транспорте, в частности велосипедных и автомобильных колесах. Они имеют форму окружности и обладают определенным диаметром, который является одной из характеристик колеса.

Окружности также используются в измерительных инструментах. Например, в технической рисовке и строительстве используются циркули, которые позволяют рисовать окружности заданного диаметра.

Таким образом, окружность является важным элементом нашей повседневной жизни. Мы встречаем ее в различных областях и сферах, начиная от архитектуры и дизайна, заканчивая транспортом и измерениями.

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 914 057 Материал в базе данных.

‘Интеграция современного искусства в детское творчество’

Сертификаты и скидки для каждого участника

Мы ищем преподавателей в команду Infowork

Другие материалы

‘Практический подход к решению проблемы потери смысла жизни: логопедия’.

Сертификаты и скидки для каждого участника

Вам будут интересны эти курсы:

• Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
• Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
• Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
• Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
• Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
• Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
• Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
• Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
• Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
• Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
• Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
• Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
• Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

Оставьте свой комментарий

• 25.09.2016 4115
• PPTX 1.7 мбайт
• 340 скачиваний
• Рейтинг: 3 из 5
• Оцените материал:

Данный материал опубликован Оксаной Коржуковой. Инфоурок — это информационный посредник, предлагающий пользователям возможность публиковать на сайте методические материалы. Пользователи, загружающие материалы на сайт, несут полную ответственность за них и содержащуюся в них информацию, а также за соблюдение авторских прав.

Если вы считаете, что материал нарушает авторские права или должен быть удален с сайта по любой другой причине, вы можете подать жалобу на материал.

Автор материала

• На сайте: 5 лет и 9 месяцев
• Подписчики: 0
• Всего просмотров: 15128
• Всего материалов: 12

Московский институт профессиональной подготовки и повышения квалификации преподавателей

Использование круга и окружности в жизни

Круг широко используется в архитектуре и строительстве. Он является одной из основных форм для создания колонн, арок и куполов. Круглые формы также часто используются в декоративных элементах интерьера, например в карнизах или осветительных приборах.

Окружность используется в различных научных и инженерных расчетах. Она является базовой геометрической фигурой для определения радиуса и диаметра объектов, а также для расчета и исследования кривых и форм. Окружности также широко применяются в области автомобильного производства, например при расчете радиуса колес и поворотного радиуса автомобиля.

Окружности и круги важны также в математике и геометрии. Они служат основой для изучения геометрических преобразований, тригонометрии, аналитической геометрии и многих других областей. Знание свойств и характеристик кругов и окружностей помогает решать различные задачи и применять геометрические принципы в реальной жизни.

Таким образом, круг и окружность имеют широкий спектр применения в различных сферах человеческой деятельности, от архитектуры и инженерии до науки и математики.

Формулы для окружности и круга

Мы рассмотрели окружности и круг, а также их элементы, однако ни одну задачу не получится решить без формул. Давайте рассмотрим их. 

Однако перед этим необходимо ввести еще несколько терминов. 

Длина окружности – это длина кривой, которая образует окружности. 

Если мы с помощью сантиметровой ленты измерим длину нашего обруча, то как раз получим длину окружности. 

Длина дуги – это длина части кривой, которая образует окружность. 

Отличие от длины окружности только в том, что тут измеряется не вся кривая, а только ее часть. 

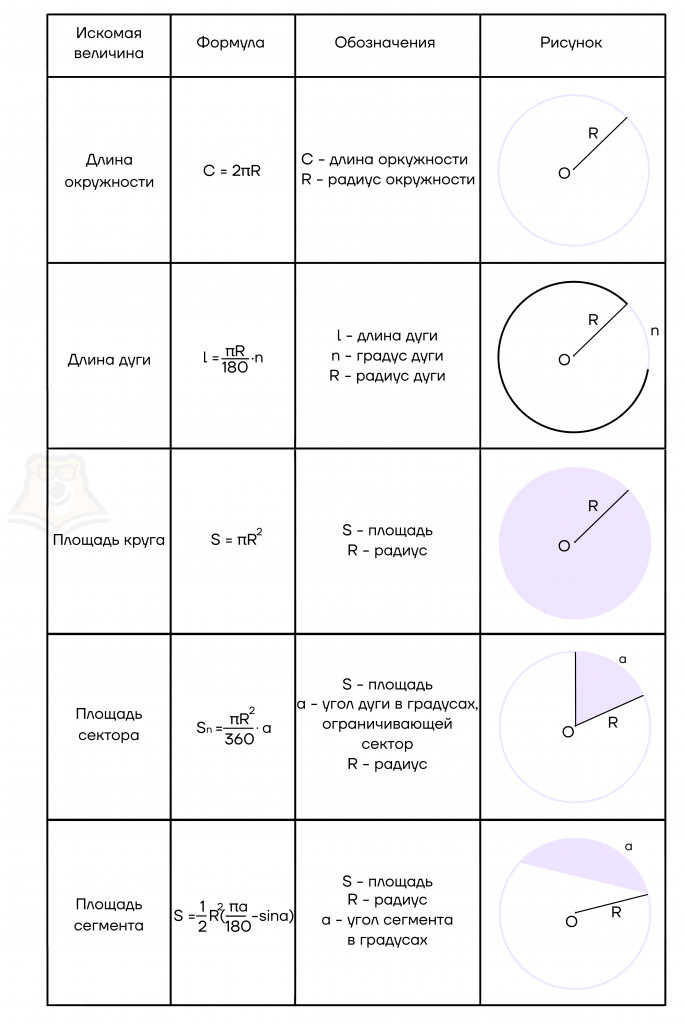
В таблице ниже приведены основные формулы, которые могут встретиться при решении задач. 

Выводы

Круг – плоская, двухмерная фигура. Шар – объемное трехмерное геометрическое тело. Тем не менее, они имеют массу сходств (наличие ограничивающей поверхности, диметра и радиуса, наполненность структуры в отличие от той же окружности, возможност вычислить площадь).

Чем же отличается круг от шара? Круг плоский, шар же имеет объем. Именно объемность шара позволяет ему делиться на сечения, которые по своей сути являются кругами. Круг, напротив, делится на сектора.

Публикации по теме:

Детско-родительский игровой сеанс «Круг» для детей ОВЗ Игровое занятие КРУГ для детей ОВЗ Тема «Осень. Природные явления» Цели и задачи занятия КРУГ Главная цель занятия КРУГ – дать каждому ребенку.

Конкурс профессионального мастерства «Солнечный круг» (фотоотчет) С 12 по 26 октября 2015 года в нашем детском саду проходил конкурс профессионального мастерства «Воспитатель года». Цель конкурса: выявление.

Конспект НОД по ФЭМП «Знакомьтесь: круг» Конспект НОД по ФЭМП во второй младшей группе «Знакомьтесь- круг» Цель: развитие познавательных интересов детей Задачи: Познакомить.

НОД по математике «Круг и квадрат» (младшая группа) Тема: «Круг и квадрат» (младшая группа) Образовательная область: познание Цель: Продолжать учить находить один и много предметов в специально.

Поделки в технике «объемный квиллинг» Здравствуйте, коллеги! Недавно открыла для себя технику объемного квиллинга. Искусство, которое на русском языке называют «бумагокручением»,.

Проект по математическому развитию «Круг, квадрат и треугольник-фигуры важные, фигуры нужные» Номинация проекта – «Дошкольный возраст» Вид проекта: долгосрочный, фронтальный. Участники проекта: подгруппа детей средней группы, воспитатель.

«Снежинка 3-D». Объемный модуль для украшения интерьера Приближаются Новогодние праздники и перед нами, как воспитателями опять стоит вопрос «Чем же удивить детей и взрослых?». Просторы Интернета.

Совместная образовательная деятельность по ФЭМП «Круг и квадрат» Совместная образовательная деятельность взрослого и детей ФЭМП «Круг и квадрат». Цель: закреплять умение различать и называть круг и квадрат.

Весенний объемный тюльпан на открытке в подарок маме Не за горами прекрасный весенний праздник 8 Марта. И уже сейчас многие педагоги задумались над тем, что бы смастерить с детьми мамам в.

Разбираемся в том что такое окружность и круг. Формула площади круга и длины окружности.

Мы каждый день встречаем множество предметов, по форме которые образовывают круг или напротив окружность. Иногда возникает вопрос, что такое окружность и чем она отличается от круга. Конечно же, мы все проходили уроки геометрии, но иногда не помешает освежить знания весьма простыми объяснениями.