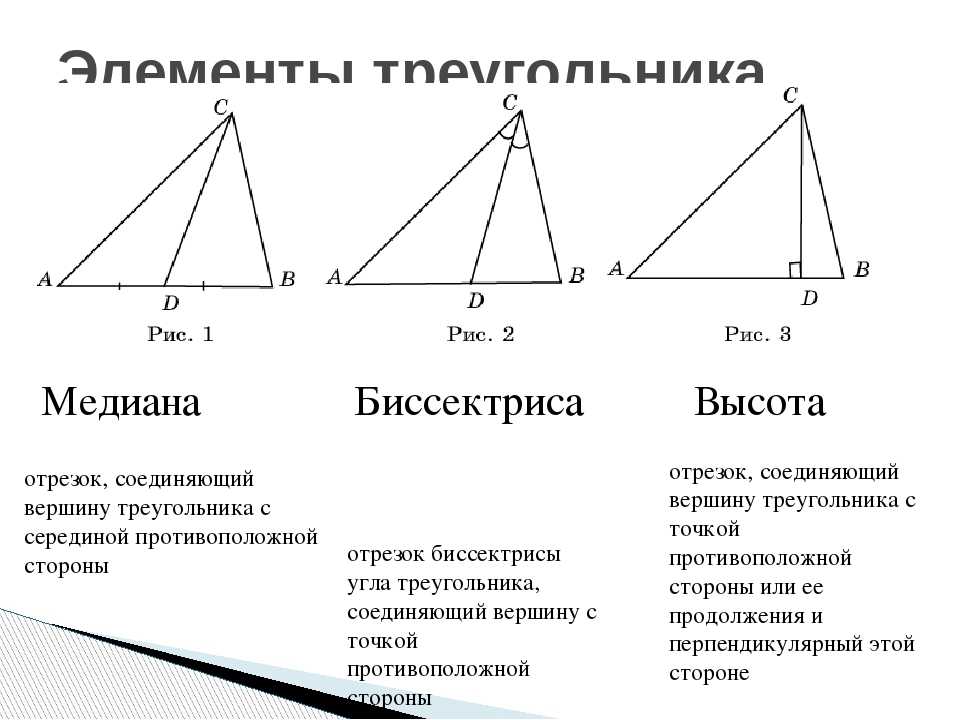
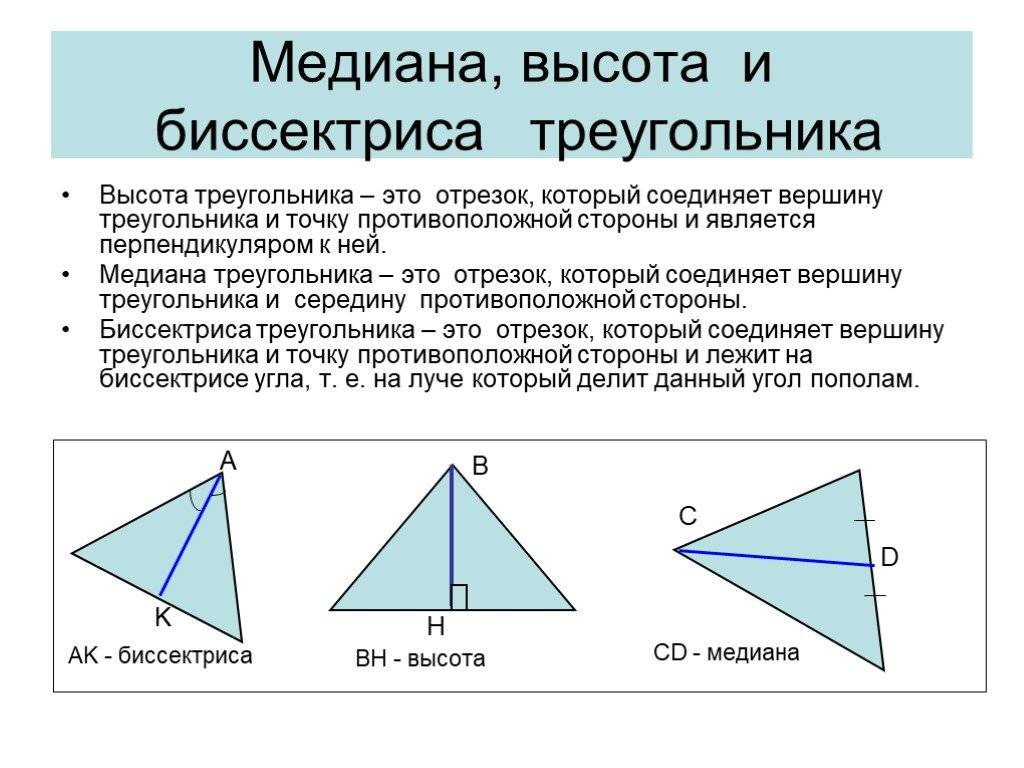
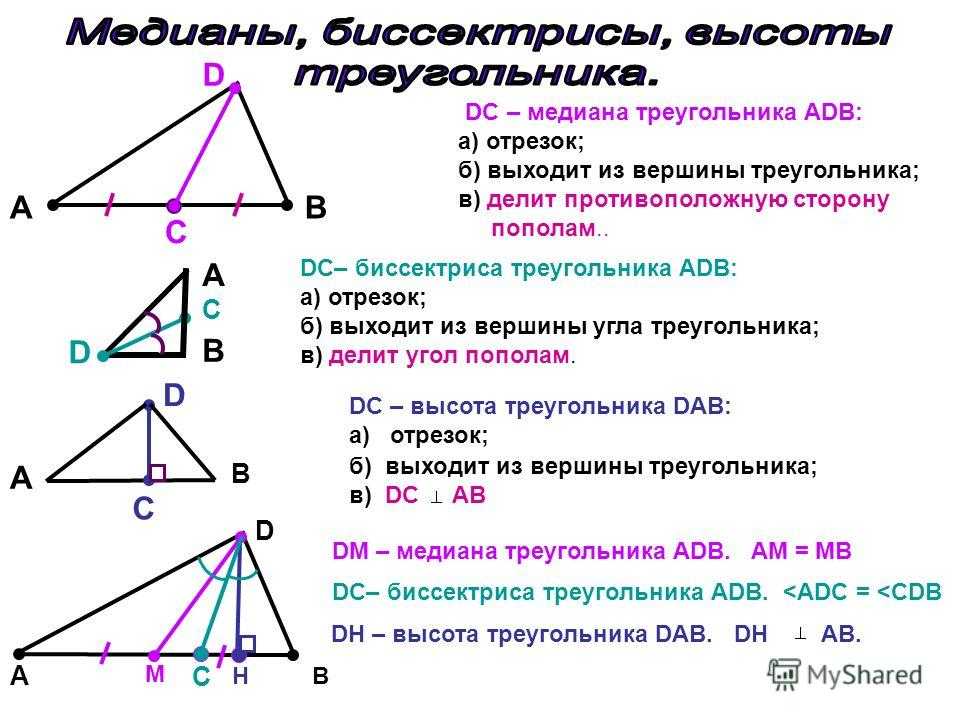
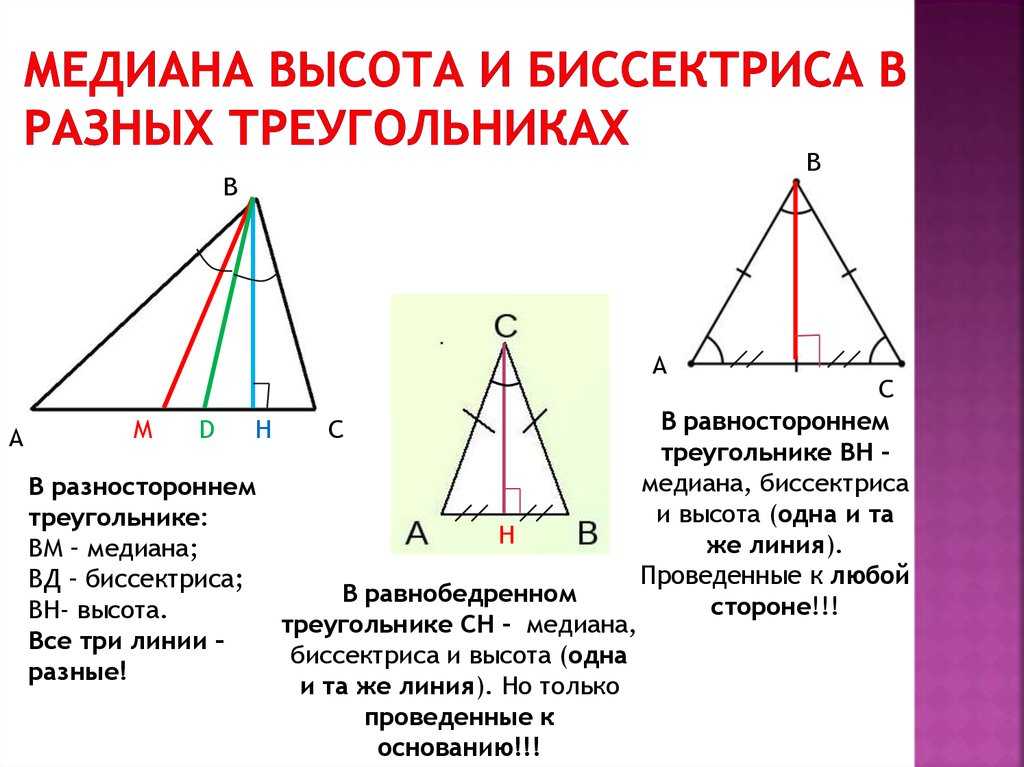
Теорема о длине медианы треугольника
Медиана треугольника определяется через три его стороны по формуле:
где a, b, c — стороны треугольника, ma — медиана, проведенная к a. С доказательством этого утверждения интересующийся читатель может ознакомиться в видеоуроке.
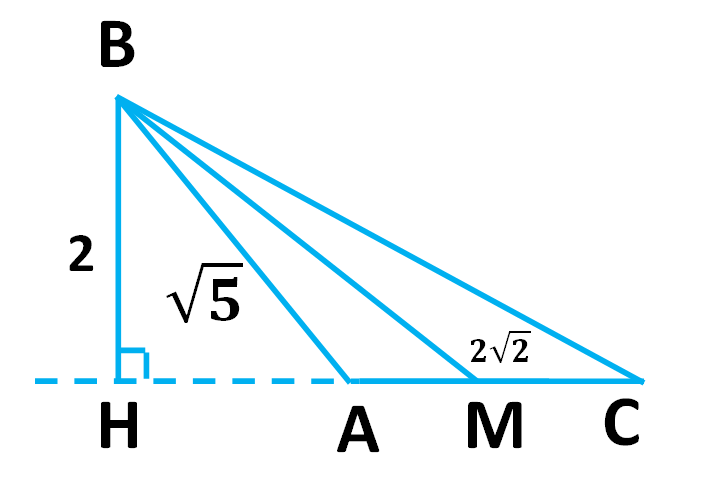
| Пример 2. В треугольнике ABC со стороной AB = из вершины B к стороне AC проведены медиана BM = и высота BH = 2. Найдите сторону BC, если известно, что ∠ B + ∠ C < 90°.
|
Решение. Из анализа условия задачи делаем вывод, что ∠ A — тупой. Действительно, ведь сумма всех углов в треугольнике равна 180°. Находим по теореме Пифагора длину HA = 1. Далее по теореме Пифагора находим длину HM = 2. Следовательно, AM = HM — HA = 1. При этом AM = MC = 1 (т. к. BM — медиана). Итак, HC = HA + AM + MC = 3. Следовательно, по теореме Пифагора BC = . Прямой подстановкой убеждаемся в справедливости ранее полученной формулы для длины медианы треугольника.
Задача для самостоятельного решения №2. В треугольнике ABC медианы, проведенные к сторонам AC и BC, пересекаются под прямым углом. Известно, что AC = b, BC = a. Найдите длину стороны AB.
Показать ответ
Ответ:
Применение медианы и биссектрисы в разных областях
Медиана — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Применение медианы в разных областях достаточно широко. Например, в математике медиана используется для нахождения медианного значения данных, что позволяет получить более репрезентативную информацию о выборке. В географии медианы применяются для определения точки равновесия распределения населения. Также медиану можно использовать в медицине для определения наиболее характерных показателей здоровья в группе пациентов.
Биссектриса — это линия, делящая угол на две равные части. Биссектриса также имеет различные применения в разных областях. В архитектуре она используется для создания симметричных и гармоничных конструкций. В физике биссектриса может быть использована для нахождения угла падения и отражения светового луча. В образовании биссектриса помогает учащимся лучше понять свойства углов и треугольников.
Таким образом, медиана и биссектриса являются важными концепциями геометрии, которые находят применение в разных областях. Они отличаются друг от друга по своему назначению и способам использования, но играют важную роль в решении различных задач.
География
Медиана — это линия, проведенная из вершины треугольника к середине противоположной стороны. Медиана делит сторону треугольника на две равные части и проходит через центр масс треугольника. Медианы используются в географии для определения центра масс географических объектов, исследования плотности населения и других параметров.
Биссектриса — это линия, которая делит угол на две равные части. В географии биссектрисы используются, например, для определения середины границы между двумя государствами или провинциями.
Отличие медианы от биссектрисы заключается в том, что медиана делит сторону треугольника, а биссектриса делит угол. Применение медианы и биссектрисы зависит от конкретной задачи в географии, но оба понятия помогают ученым и исследователям анализировать и описывать различные аспекты нашей планеты и ее географических объектов.
Архитектура
Различие между медианой и биссектрисами заключается в их направлении и функциях. Медиана направлена от вершины к середине противоположной стороны и используется для распределения и равномерного расположения элементов. Биссектрисы направлены от угла треугольника к противоположной стороне и служат для создания симметричных и сбалансированных форм.
В архитектуре медианы и биссектрисы применяются для создания гармоничного и пропорционального дизайна. Они помогают уравновесить элементы по горизонтали и вертикали, создать симметрию и достичь эстетического баланса. Эти линии помогают архитекторам создавать привлекательные и удобные пространства, которые приятно воспринимать как визуально, так и функционально.
Медицина
Медиана — это статистический показатель, который используется для нахождения среднего значения в наборе данных. В медицине медиана может быть использована для определения среднего значения какой-либо характеристики у большой группы пациентов.
Однако, медицина отличается от медианы не только в использовании статистических показателей. Медицина — это комплекс научных, профессиональных и практических знаний, которые направлены на сохранение и восстановление здоровья людей.
Основными целями медицины являются предотвращение, диагностика и лечение заболеваний, а также поддержание и улучшение общего физического и психического состояния человека.
Медицина включает в себя различные специальности, такие как терапия, педиатрия, хирургия, неврология, гинекология и другие. Каждая специальность имеет свои особенности и применяет свои методы для диагностики и лечения пациентов.
Все врачи и медицинский персонал, работающие в области медицины, должны иметь высокую квалификацию и навыки, чтобы предоставлять качественную медицинскую помощь своим пациентам.
Вместе с тем, медицина постоянно развивается и совершенствуется. Врачи и ученые работают над разработкой новых методов диагностики и лечения, а также над открытием новых лекарственных препаратов.
Отличие медицины от медианы заключается не только в применении определенных показателей и методов. Медицина — это сложная и важная область, которая направлена на сохранение и повышение здоровья человека.
Медицина играет огромную роль в нашей жизни и оказывает влияние на все сферы общества. Благодаря медицине люди имеют возможность лечиться и продолжать вести полноценный и здоровый образ жизни.
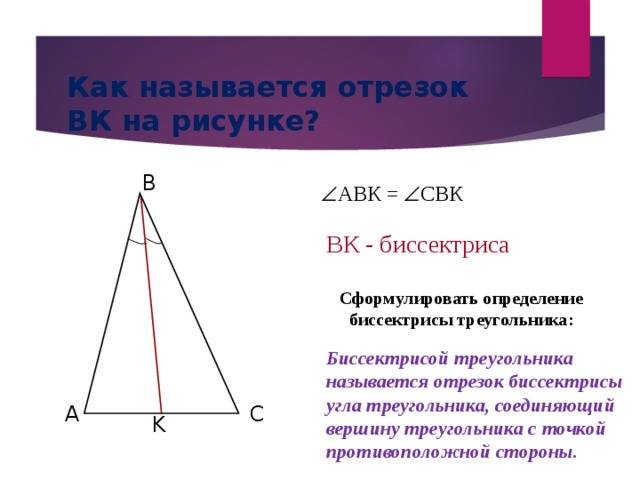
Биссектриса угла треугольника
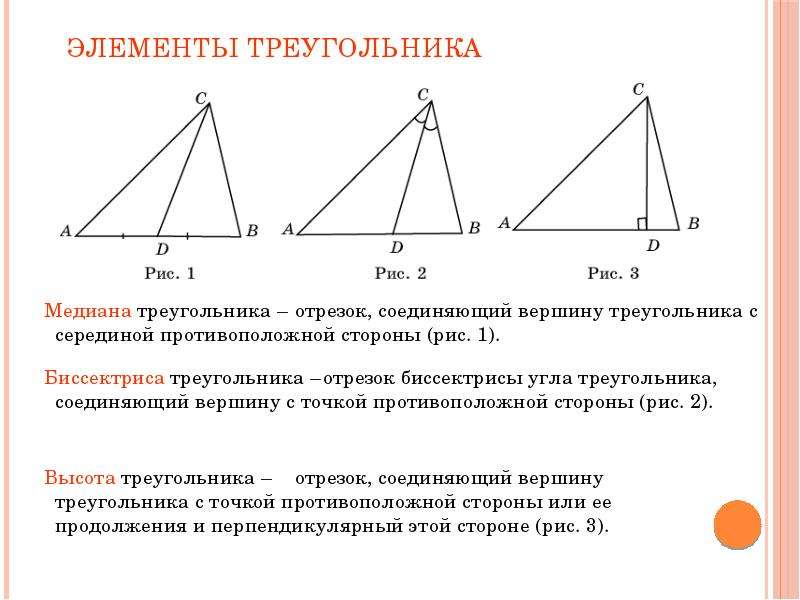
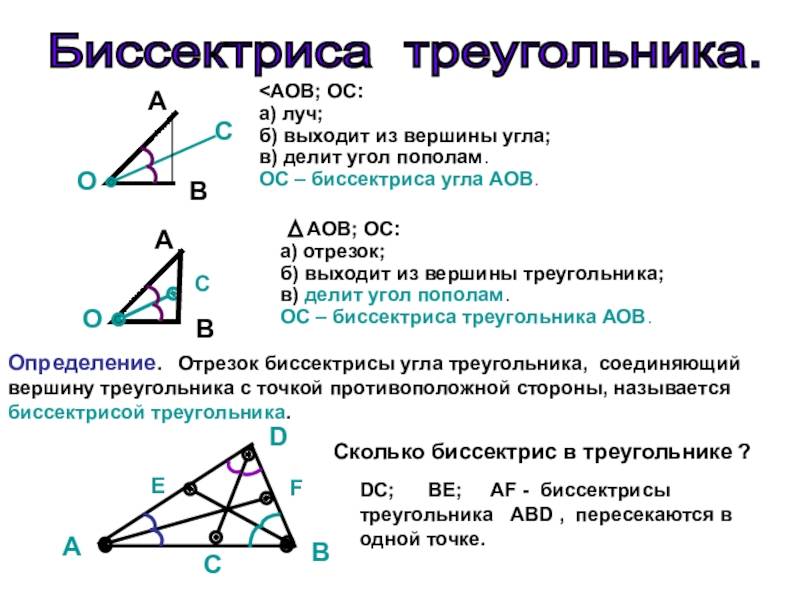
Пусть нам дан треугольник $\bigtriangleup{ABC},$ где из вершины $C$ к противолежащей стороне $AB$ опущен отрезок $CD$ таким образом, что $\angle{C}$ делится отрезком $CD$ на два равных друг другу угла. Тогда отрезок $CD$ будет называться биссектрисой угла треугольника $\bigtriangleup{ABC}$ (от лат. ‘bi’ — «два», ‘secare’ — «резать»).
По аналогии с высотами, биссектриса угла треугольника опускается как из вершины $A$, так и из вершины $B$.
Дадим определение:
В отличие от высоты, биссектриса — понятие, теснее связанное с углом, чем с треугольником, поэтому ряд ее свойств больше определяет геометрию углов, чем геометрию треугольников. Например, одно из таких замечательных свойств связано со . Оказывается, что биссектрисы, проведенные из смежных углов, будут образовывать прямой угол. Давайте это докажем!
Доказательство. $\angle{AOC}$ является смежным с $\angle{COE}$. $OB$ — биссектриса $\angle{AOC};$ $OD$, соответственно, биссектриса $\angle{COE}$. По свойству смежных углов известно, что сумма смежных углов равняется $180^{\circ}$. То есть:
$$\angle{AOC}+\angle{COE}=180^{\circ}.$$
Согласно условию $\angle{AOB}=\angle{BOC}=\frac{\angle{AOC}}{2}$, $\angle{COD}=\angle{DOE}=\frac{\angle{COE}}{2}$. Тогда уравнение выше можно представить в следующем виде:
$$2\angle{BOC}+2\angle{COD}=180^{\circ}$$
Разделим обе части уравнения на $2$ и получим: $\angle{BOC}+\angle{COD}=90^{\circ}.$ $\angle{BOC}+\angle{COD}$ равняется $\angle{BOD}$. Теорема доказана.
{"questions":[{"content":"`image-1`Даны $\\angle{AOB}, \\angle{BOC}$ и биссектрисы к углам $OP$ и $OK$ соответственно. Угол $\\angle{AOB}$ — смежный с $\\angle{BOC}$. Известно, что $\\angle{AOP}=15^{\\circ}$. Чему равняется $\\angle{KOC}?$ `input-7`","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/02/test-2.svg","width":"500"},"input-7":{"type":"input","answer":"75"}},"step":1,"hints":}]}Свойства биссектрисы в треугольнике
Основные свойства биссектрисы в треугольнике:
- Биссектриса является биссектрисой угла в вершине треугольника.
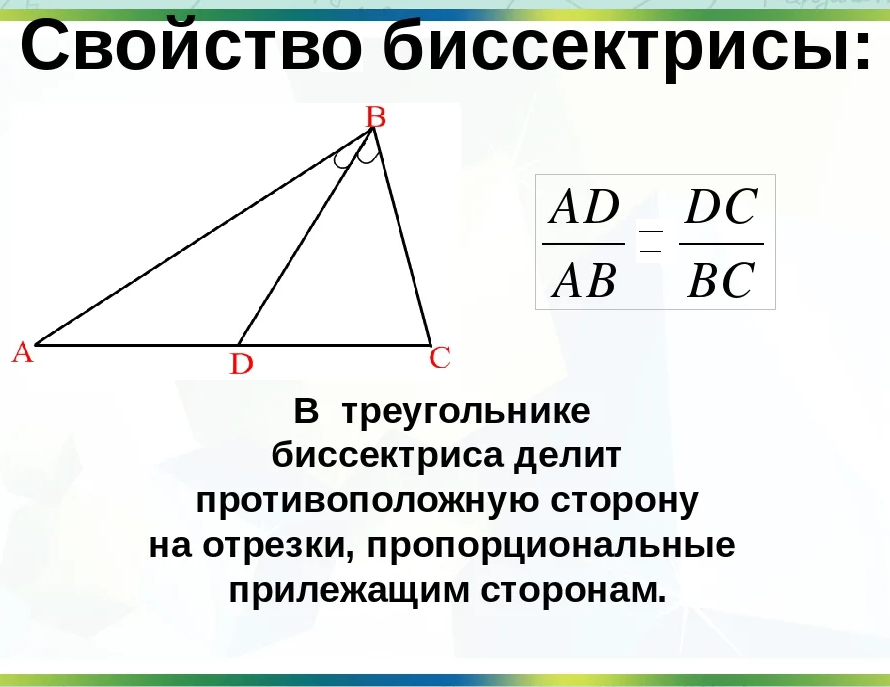
- Биссектриса делит противоположную сторону треугольника на две отрезка, пропорциональные длинам смежных сторон.
- Точка пересечения биссектрис треугольника образует центр вписанной окружности.
- Длины биссектрис треугольника обратно пропорциональны длинам противоположных сторон.
- Сумма длин двух биссектрис треугольника равна длине третьей биссектрисы.
- Биссектриса является внутренним угловым биссектором треугольника.
- Окружность, описанная вокруг треугольника, проходит через точку пересечения биссектрис треугольника.
Используя свойства биссектрисы треугольника, можно решать задачи на нахождение длин сторон или углов треугольника, а также нахождение радиусов вписанной и описанной окружностей.
Применение биссектрисы в треугольнике
Применение биссектрисы в треугольнике имеет несколько важных аспектов:
1. Определение угла: Биссектриса может использоваться для определения угла в треугольнике. Для этого достаточно провести биссектрису угла и измерить угол между биссектрисой и противоположной стороной треугольника.
2. Построение биссектрисы: Биссектрису можно построить в треугольнике с помощью рисования перпендикуляра к противоположной стороне из вершины угла. Это может быть полезно при конструировании геометрических фигур или нахождении центра вписанной окружности.
3. Разделение стороны на отрезки: Биссектриса также может быть использована для разделения стороны треугольника на отрезки в определенных пропорциях. Если биссектриса делит сторону на два отрезка, то отношение длин этих отрезков равно отношению длин смежных сторон треугольники.
Применение биссектрисы в треугольнике является одним из важных понятий геометрии. Это позволяет углубить понимание треугольников и их свойств, а также применять знания в практических ситуациях, связанных с измерением углов и построением различных геометрических фигур.
Классификация треугольников по сторонам
Равносторонний треугольник
Равносторонний треугольник или правильный треугольник – это треугольник, у которого все стороны равны. У равностороннего треугольника все углы равны 60°.
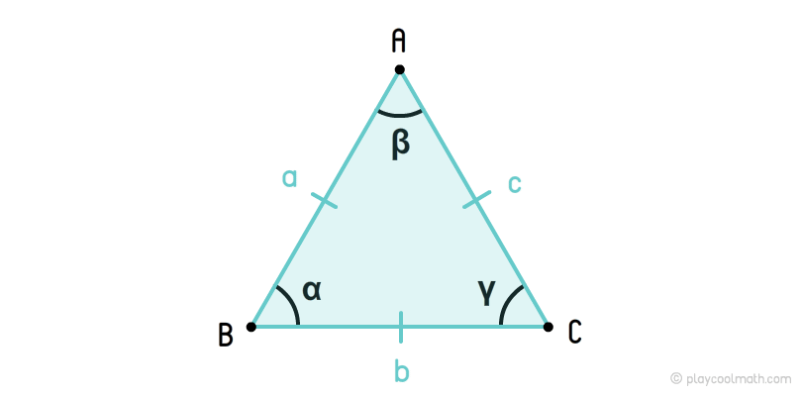
На рисунке мы обозначили стороны как a, b, c, где a = b = c. Углы обозначили как α, β, γ, где α = β = γ = 60°. Одинаковые стороны помечаются одинаковым количеством черточек. Мы пометили стороны a, b, c одной чертой. Одинаковые углы помечаются одинаковым количеством дуг. На рисунке мы все углы пометили одной дугой.
Неравносторонний треугольник
Неравносторонний треугольник – это треугольник, у которого все стороны не равны. У неравностороннего треугольника углы тоже не равны.
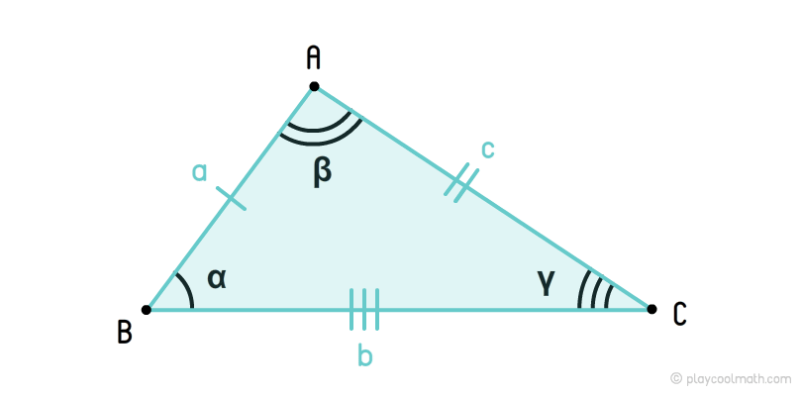
На рисунке мы обозначили стороны a, b, c, где a ≠ b ≠ c. Углы обозначили как α, β, γ, где α ≠ β ≠ γ. Мы пометили стороны a, b, c разным количеством черточек, указав что все стороны имеют разную длину. Все углы пометили разным количеством дуг, указав, что все углы имеют разные угловые меры.
Равнобедренный треугольник
Равнобедренный треугольник – это треугольник, у которого две стороны равны. Эти стороны называются боковыми или бедрами, а третья сторона называется основанием.
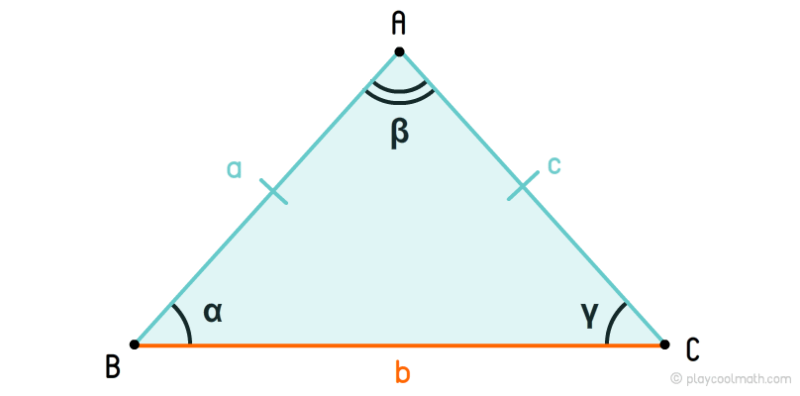
На рисунке мы обозначили боковые стороны как a, c, где a = c, а основание b, где b ≠ a и b ≠ c. У равнобедренного треугольника углы у основания равны α = γ.
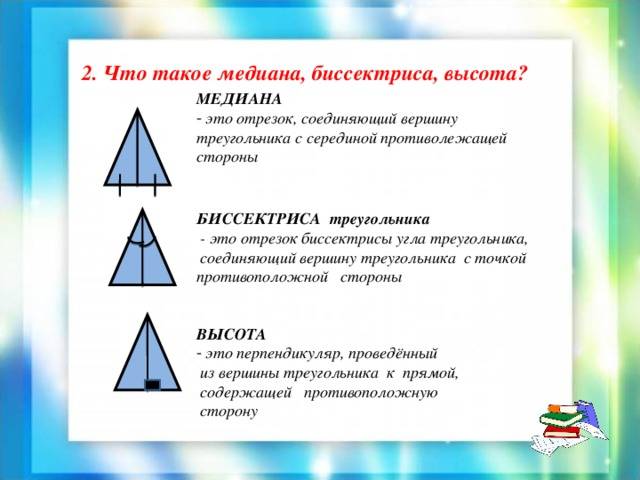
Медиана
Наконец, проведем отрезок $CD$ в треугольнике $\bigtriangleup{ABC}$ из вершины $C$ к противолежащей стороне $AB$ таким образом, что сторона $AB$ поделится на два равных друг другу отрезка. Мы получили третий важный отрезок в треугольнике — медиану (от лат. ‘medianus’ — «средний»).
По определению:
{"questions":[{"content":"`image-1` Есть три треугольника. Есть три отрезка — медиана, высота и биссектриса. Попробуйте определить, где какой отрезок проведен. <br />`matcher-4`","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/02/test-3.svg"},"matcher-4":{"type":"matcher","labels":,"items":}}}]}Обратили внимание?
Медианы, как и биссектрисы с высотами, пересекаются в одной точке внутри треугольника. Исключением является тупоугольный треугольник и его высоты: высоты в тупоугольном треугольнике пересекаются вне треугольника.
Доказать это, к сожалению, нам пока не по силам, ибо требуется знание нескольких важных теорем, которые мы обязательно изучим в курсе далее. Как только, так сразу. Пока — принять, понять, поверить, что медианы треугольника пересекаются в одной точке.
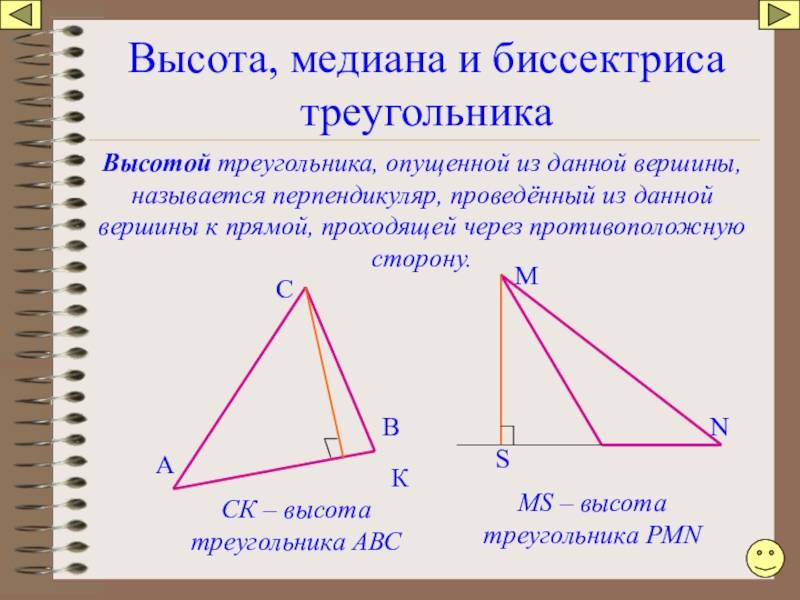
Высота треугольника
Пусть нам дан треугольник $\bigtriangleup{ABC},$ где из вершины $C$ к противолежащей стороне $AB$ опущен отрезок $CD$, образующий при этом перпендикуляр к стороне $AB$. Тогда отрезок $CD$ будет являться высотой треугольника $\bigtriangleup{ABC}$. Аналогичный перпендикуляр можно опустить как из вершины $A$, так и из вершины $B$.
Получается, что:
В остроугольном треугольнике — где углы имеют значение $<90^{\circ}$ — чертеж высот не вызывает сложности: они всегда будут пересекаться внутри треугольника. Однако если треугольник тупоугольный — один из углов имеет значение $>90^{\circ},$ — провести высоту будет уже не так интуитивно просто.
Осмотрите треугольник $\bigtriangleup{PMK}$ выше, с тупым углом $\angle{M}$.
Нам необходимо провести высоту из вершины $K$ к стороне $PM$. Подумайте, как будет располагаться отрезок, выполните чертеж и сравните свои предположения со скрытым чертежом.
Пересечение высот: как найти высоту треугольника
Выходит, что в остроугольном треугольнике высоты пересекаются в точке, расположенной строго внутри треугольника — никаких дополнительных построений не требуется.
Высоты в тупоугольном треугольнике пересекаются в точке, расположенной вне треугольника, — чтобы найти высоту треугольника, необходимо достраивать продолжение сторон
Так, в случае с нашим тупоугольным треугольником, высоты пересекаются в точке $O$ — внимание на чертеж выше
{"questions":[{"content":"`image-1` Помимо остроугольного и тупоугольного треугольника, существует треугольник прямоугольный — частный случай, когда один из углов прямой, то есть равняется $90^{\\circ}$. Что это за треугольник и какими свойствами он обладает, подробнее мы разберем далее в курсе геометрии. Пока что давайте просто поразмышляем: а где же будут <b>пересекаться высоты</b> в прямоугольном треугольнике? `choice-11`","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/02/test-right.svg","width":"500"},"choice-11":{"type":"choice","options":,"explanations":["","","","Это очень логично! <br /><br />В треугольнике $\\bigtriangleup{ABC}$ сторона $AB$ является высотой к стороне $BC$, и наоборот, ведь $\\angle{B}$ — прямой. Высота к стороне $AC$ будет выходить из вершины $B$. Так что точка пересечения высот в прямоугольном треугольнике, получается, располагается в точке $B$ — в вершине прямого угла."],"answer":}}}]}Биссектриса и высота: сравнение и отличия
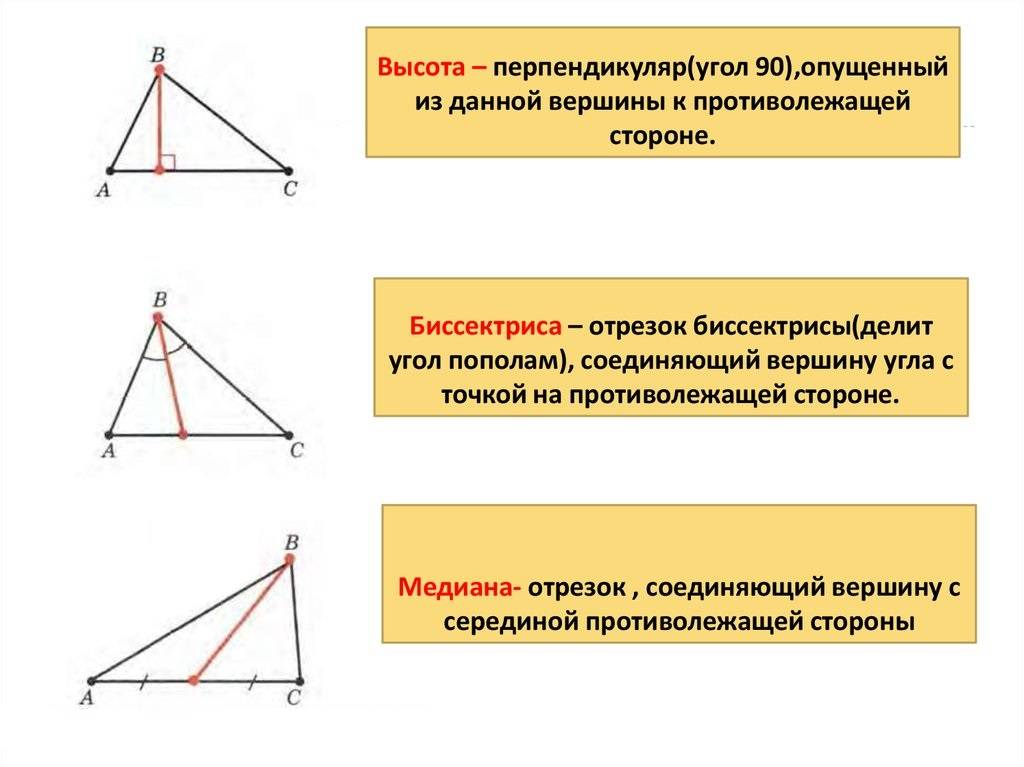
Биссектриса треугольника — это линия, которая делит угол треугольника пополам. Она проходит через вершину угла и делит противоположную сторону на две равные части. Биссектриса может быть внутренней, когда угол делится на две части внутри треугольника, или внешней, когда угол делится на две части вне треугольника. Биссектриса имеет важные геометрические свойства и может быть использована для нахождения длин сторон треугольника.
Высота треугольника — это перпендикуляр, проведенный из вершины треугольника к основанию или его продолжению. Высота проходит через вершину и перпендикулярна определенной стороне или продолжению этой стороны
Высота делит треугольник на два прямоугольных треугольника и имеет важное значение для решения задач связанных с площадью и объемом треугольника
Главное отличие между биссектрисой и высотой заключается в их определении и функциональных значениях. Биссектриса делит угол пополам и может быть использована для нахождения длин сторон треугольника. Высота же является перпендикулярной линией и может быть использована для нахождения площади треугольника. В отличие от биссектрисы, высота не делит угол, а перпендикулярна стороне треугольника.
Медиана отличается от биссектрисы и высоты следующими особенностями:
— Медиана является отрезком, соединяющим вершину треугольника с серединой противоположной стороны.
— Медиана делит соответствующую сторону треугольника на две равные части.
— Медиана пересекает противоположную боковую сторону в точке, которая является серединой этой стороны.
— Биссектриса является лучом, исходящим из вершины треугольника и делящим соответствующий угол на два равных угла.
— Биссектриса пересекает противоположную сторону в точке, которая делит ее в отношении длин окружающих сторон.
— Высота является перпендикулярной отрезком, исходящим из вершины треугольника и перпендикулярным граням соответствующей стороны.
— Высота пересекает противоположную сторону в точке, которая является перпендикулярной проекцией вершины на эту сторону.
Медиана, биссектриса и высота выполняют разные функции в треугольнике и имеют свои уникальные свойства, которые полезны при решении геометрических задач.
Свойства биссектрисы треугольника
1. Каждая точка этой линии равноудалена от сторон угла. Часто эту характеристику выбирают в качестве определения, поскольку верно и обратное утверждение для любого произвольного треугольника. Это позволяет находить и радиус вписанной окружности.
2. Все внутренние отрезки, делящие углы пополам, пересекаются в одной точке, которая является центром окружности, вписанной в фигуру, т. е. точка пересечения находится на равных расстояниях от сторон.
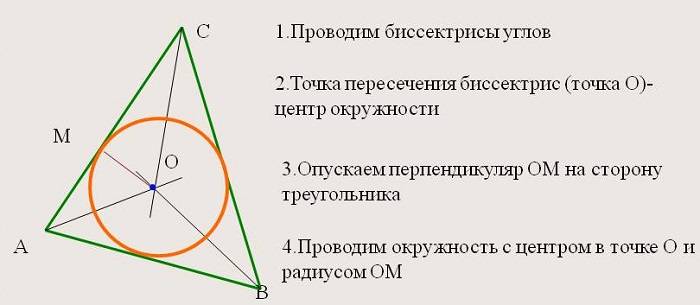
Данное свойство позволяет решать целый класс разнообразных задач, выводить формулы для радиусов вписанных окружностей правильных многоугольников.
Благодаря этому утверждению, легко доказывается следующее правило:
Площадь описанного многоугольника равна:
S = p∗r
где p – полупериметр, а r – радиус вписанной окружности.
Это позволяет находить решение не только планиметрических, но и стереометрических задач.
Важную роль играют внешние биссектрисы треугольника. Вместе с внутренними они образуют прямые углы;
3. Сумма величин двух прилежащих сторон, делённая на длину противолежащей стороны, задаёт отношение частей биссектрисы (считая от вершины), полученных точкой пересечения всех трёх соответствующих линий.
Некоторые виды геометрических фигур, в силу своих особенностей, порождают особые примечательные характеристики;
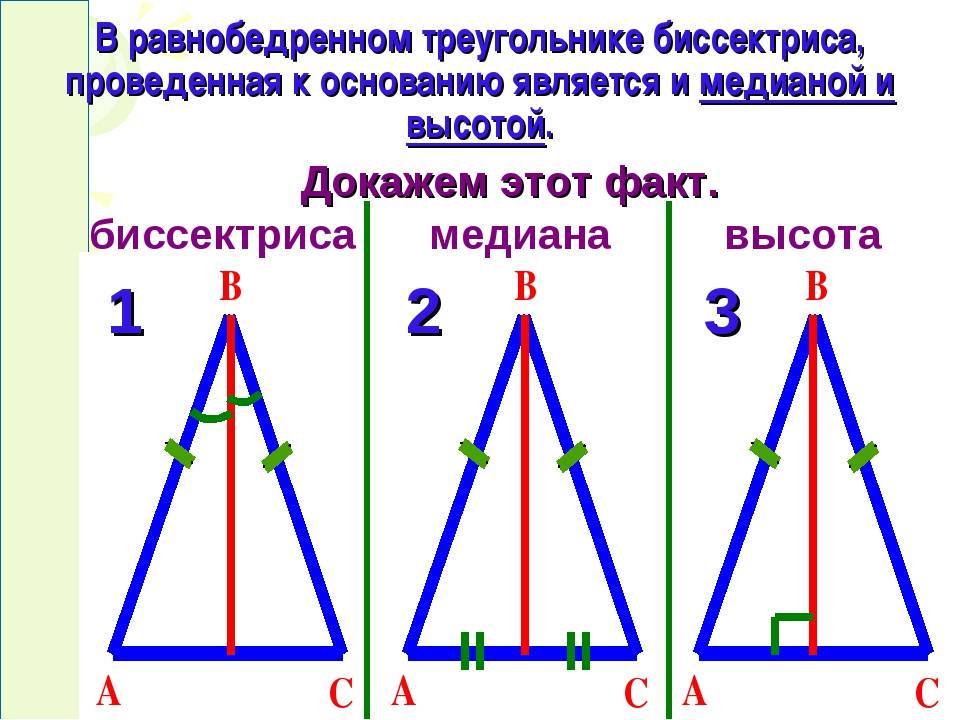
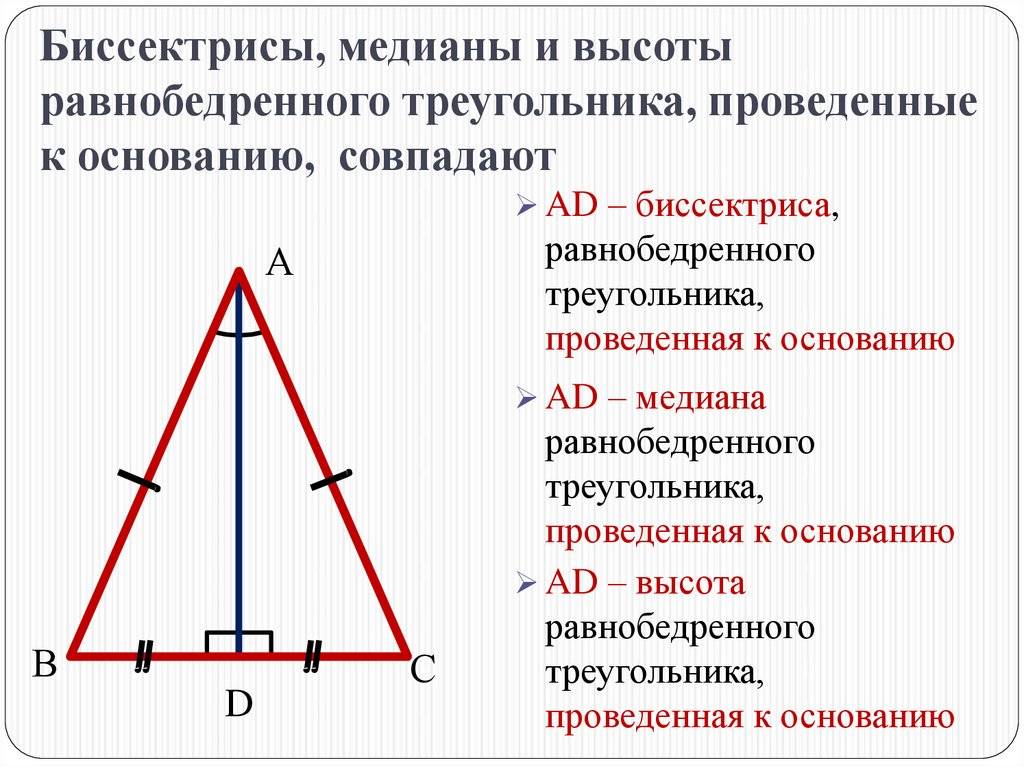
4. В равнобедренном треугольнике биссектриса, проведённая к основанию, одновременно является медианой и высотой. Две другие – равны между собой.
В этом случае основание параллельно внешней биссектрисе.
Обратное положение также имеет место. Если прямая проведена параллельно основанию равнобедренного треугольника через некоторую вершину, то внешняя биссектриса при этой вершине является частью этой линии;
5
Для равностороннего многоугольника важной характеристикой считается равенство всех биссектрис;. 6
У правильного треугольника все внешние биссектрисы параллельны сторонам;
6. У правильного треугольника все внешние биссектрисы параллельны сторонам;
7. Выделяют несколько особенностей, среди которых есть следующая теорема:
«Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам».
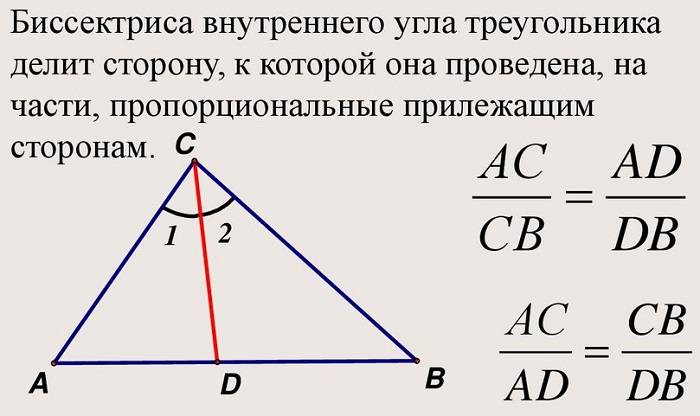
Обратное утверждение («Прямая делит сторону на отрезки, пропорциональные двум другим сторонам») выражает признаки того, что рассматриваемая линия является внутренней биссектрисой;
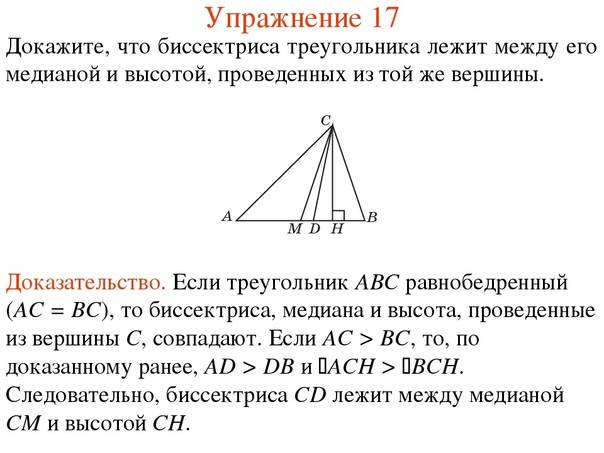
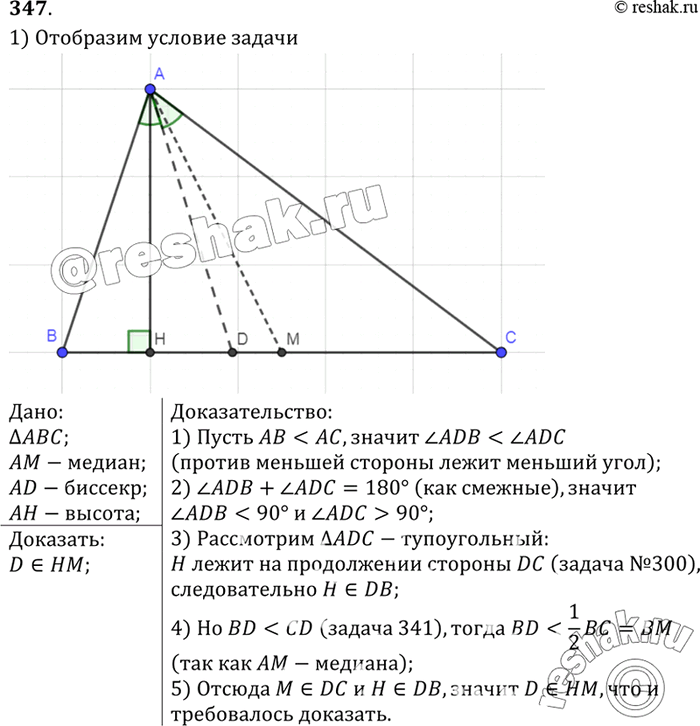
8. Разносторонний треугольник позволяет определить взаимное расположение его высоты, медианы и биссектрисы, проведённых из одной точки. В частности, медиана и высота располагаются по разные стороны от третьей линии.
Пример задач
Пример 1
Пусть дан треугольник $ABC$. Доказать, что если в нем $BD$ будет и высотой и медианой, то $AB=BC$.
Доказательство
Изобразим рисунок по условию задачи (рис. 5).
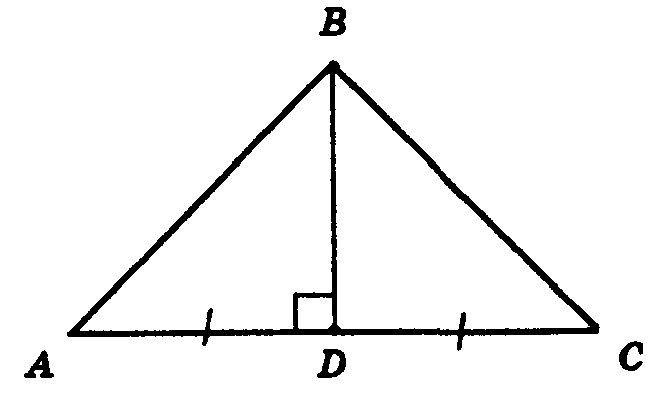
Так как $BD$ является медианой, то по определению 4 будет верно равенство
$AD=DC$
Так как $BD$ является высотой, то по определению 6 будет верно равенство
$∠ADB=∠BDC=90^0$
У треугольников $ADB$ и $BDC$ сторона $BD$ будет общей, следовательно, по всему сказанному выше эти треугольники равняются по первому признаку. Но тогда и стороны $AB$ и $BC$ равны.
Пример 2
Пусть нам даны равные треугольники $ABC$ и $A’B’C’$. В них проведены высоты $BH$ и $B’H’$, соответственно. Доказать, что эти высоты в треугольниках будут равны между собой.
Доказательство.
Изобразим рисунок по условию задачи (рис. 6).
Так как данные треугольники равны, то будет верно равенство
$∠A=∠A’$
Так как $BH$ и $B’H’$ являются высотами, то по определению 6 будет верно равенство
$∠AHB=∠A’H’B’=90^0$
Из треугольника $ABC$, имеем
$∠ABH=180^0-90^0-∠A=90^0-∠A$
Из треугольника $A’B’C’$ и равенства углов $∠A$ и $∠A’$, получим
$∠A’B’H’=180^0-90^0-∠A’=90^0-∠A’=90^0-∠A=∠ABH$
По всему сказанному выше, треугольники $AHB$ и $A’B’H’$ равняются по первому признаку. Но тогда и стороны $BH$ и $B’H’$ равны.
Функции биссектрисы треугольника
1. Определение вершины угла: Биссектриса показывает точное местоположение вершины угла треугольника.
2. Определение равных углов: Биссектриса делит угол на две равные части, поэтому каждая из половинок угла будет иметь одинаковые измерения.
3. Построение вспомогательных линий: Биссектриса может использоваться для построения других линий или точек в треугольнике. Например, пересечение биссектрис двух углов треугольника даст центр окружности, описанной вокруг треугольника.
| Функция | Описание |
|---|---|
| Определение вершины угла | Биссектриса показывает точное местоположение вершины угла треугольника. |
| Определение равных углов | Биссектриса делит угол на две равные части, поэтому каждая из половинок угла будет иметь одинаковые измерения. |
| Построение вспомогательных линий | Биссектриса может использоваться для построения других линий или точек в треугольнике. Например, пересечение биссектрис двух углов треугольника даст центр окружности, описанной вокруг треугольника. |
Все эти функции делают биссектрису треугольника важным инструментом для решения геометрических задач и изучения свойств треугольников.
Медиана треугольника: практическое применение
Одно из основных практических применений медианы треугольника — нахождение центра тяжести объекта. Если представить треугольник как плоскую фигуру, где его стороны — это участки тонкого и гибкого материала, то медиана будет показывать линию, по которой этот объект распределит свой вес равномерно.
Такое свойство медианы делает ее полезным инструментом в различных областях, связанных с равномерным распределением нагрузки. Например, в строительстве медиану треугольника можно использовать для нахождения центра масс балки или другой конструкции. Это будет полезно при расчете нагрузки на опоры и определении оптимального дизайна конструкции.
Еще одно практическое применение медианы треугольника — определение положения массы в технике и спорте. Например, при разработке автомобилей медиана треугольника может использоваться для определения центра тяжести автомобиля. Это помогает инженерам создавать более устойчивые и безопасные автомобили.
В спорте медиана треугольника применяется, например, в гимнастике. Медианы треугольников, образованных конечностями гимнаста, используются для балансировки и повышения устойчивости тела.
Таким образом, медиана треугольника имеет практическое применение в различных областях, где важна равномерная распределенная нагрузка или определение положения массы. Это делает ее важным инструментом для инженеров, архитекторов, спортсменов и других специалистов, работающих в этих сферах.
Медиана, биссектриса и высота: сравнение и отличия
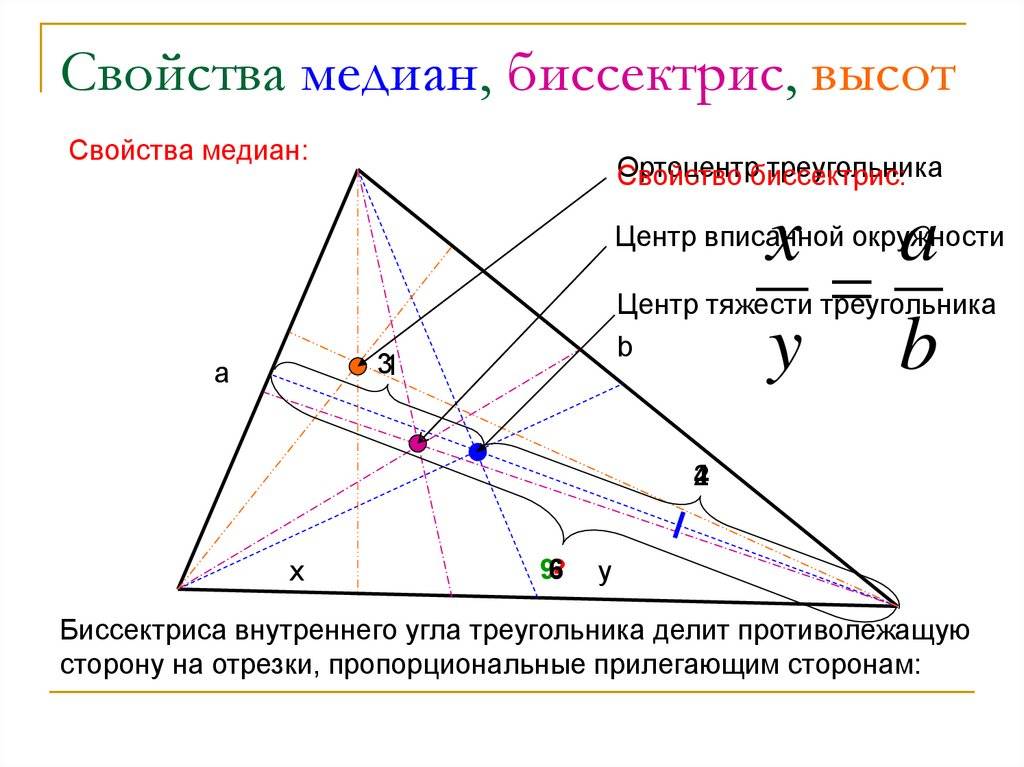
Медиана — это линия, проходящая через центр масс треугольника и соединяющая вершину с противоположным отрезком. Медианы пересекаются в одной точке, называемой центром масс или барицентром треугольника. Медианы разделяются этой точкой в отношении 2:1, то есть делятся на две одинаковые части в ближайшей точке к вершине и на одну часть в противоположной точке.
Биссектриса — это линия, которая разделяет угол треугольника на две равные части. Каждый угол треугольника имеет свою биссектрису, и они пересекаются в одной точке, называемой центральной точкой биссектрисы. Центральная точка биссектрисы находится на одинаковом расстоянии от всех сторон треугольника.
Высота — это перпендикуляр, проведенный от вершины треугольника до противоположной стороны или ее продолжения. Высоты пересекаются в одной точке, называемой ортоцентром треугольника. Ортоцентр может находиться внутри треугольника, на его сторонах или за их пределами.
| Понятие | Свойства | Пункт пересечения |
|---|---|---|
| Медиана | Делится в отношении 2:1 | Центр масс или барицентр |
| Биссектриса | Делит угол на две равные части | Центральная точка биссектрисы |
| Высота | Перпендикуляр к стороне или ее продолжению | Ортоцентр |
Итак, медиана, биссектриса и высота — это разные линии, имеющие свои уникальные свойства и пункты пересечения. Они служат важными инструментами в изучении треугольников и помогают нам понять их структуру и связи между сторонами и углами.