Чем отличается круг от шара?

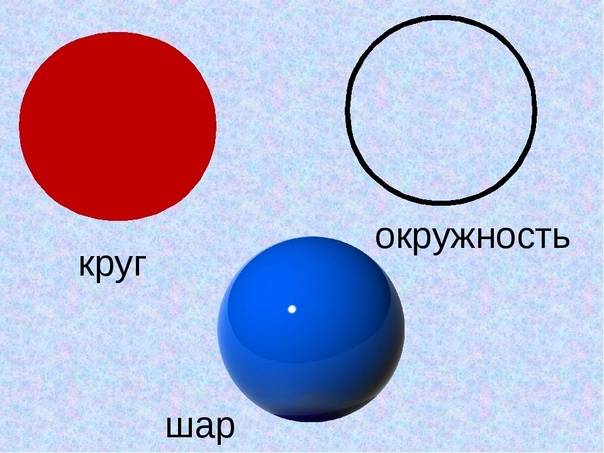
Касательная плоскость к сфере

Плос-ть, имеющая со сферой строго одну общую точку, именуется касательной плоскостью к сфере.

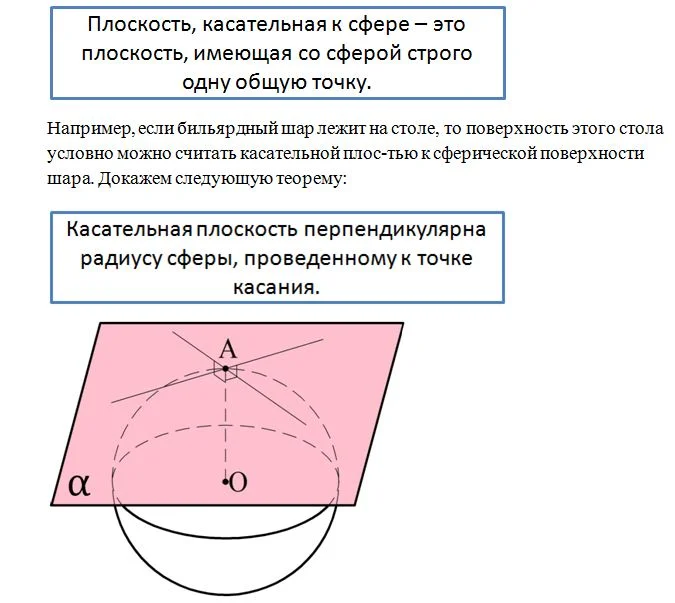
Действительно, если плос-ть касается окруж-ти, то точка касания А должна располагаться на расстоянии R от центра сферы О, где R– радиус сферы. Все остальные точки касательной плос-ти находятся вне пределов сферы, то есть должны находиться от О на расстоянии, превышающем R. Это значит, что отрезок ОА должен быть кратчайшим отрезком, соединяющим О и касательную плос-ть. Но мы знаем, что кратчайший отрезок между плос-тью и точкой – это как раз перпендикуляр, опущенный из точки на плос-ть.

Справедливо и обратное утверждение:

Доказательство. Если радиус ОА – перпендикуляр к плос-ти α, то он является кратчайшим расстоянием между плос-тью и центром О. Тогда все остальные точки плос-ти располагаются на большем расстоянии от О, чем точка А. Это значит, что они не располагаются на сфере. Значит, у сферы и плос-ти α одна общая точка А, а потому α по определению – касательная плос-ть.

По аналогии с касательной плос-тью существует понятие касательной прямой к сфере.

Касательная к сфере обладает почти теми же свойствами, что и касательная к окруж-ти.

Доказательство. Пусть m– касательная прямая к сфере с центром О. обозначим точку касания как А. Далее через прямую m и центр О проведем плос-ть α. Нам надо показать, что ОА⊥m:

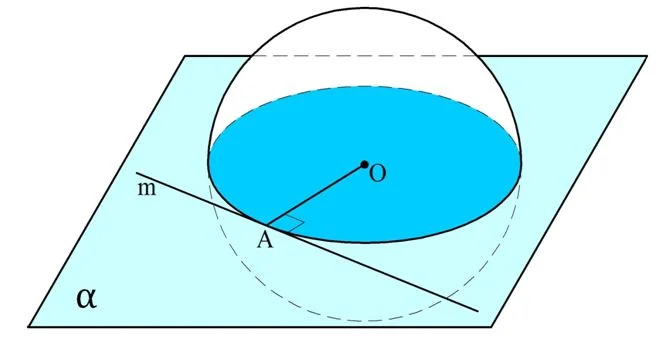
Плос-ть α будет диаметральной плос-тью. Сечение будет иметь форму окруж-ти с центром О и радиусом ОА. Прямая m будет касательной к этой окруж-ти, ведь она имеет с ней общую точку А, а второй общей точки m и окруж-ть иметь не могут, ведь такая бы точка была бы также общей для m и сферы, а m по определению имеет лишь одну общую точку со сферой. Напомним, что касательная к окруж-ти перпендикулярна радиусу, то есть m⊥ОА, ч. т. д.

Будет верным и обратное утверждение:

Для доказательства используем ту же картинку. Известно, что m⊥ОА, надо показать, что m– касательная к сфере. Проведем через пересекающиеся прямые m и ОА плос-ть α. Она снова окажется диаметральной плоскостью, и снова сечением будут окруж-ть с радиусом ОА. По признаку касательной, который мы изучали в планиметрии, m– касательная к этой окруж-ти, ведь m⊥ОА. То есть в плос-ти α есть лишь одна общая точка m и сферы. В других плос-тях у них не может быть общих точек, так как m полностью принадлежит α. В итоге у m и сферы только одна общая точка, а потому m– касательная к сфере, ч. т. д.

Рассмотрим ещё одно утверждение:

Сначала разберемся с понятием отрезков касательных. Пусть из точки А, лежащей вне сферы, к ней проведены две касательные, а точки касания обозначены буквами В и С. Тогда АВ и АС как раз и будут отрезками касательных:

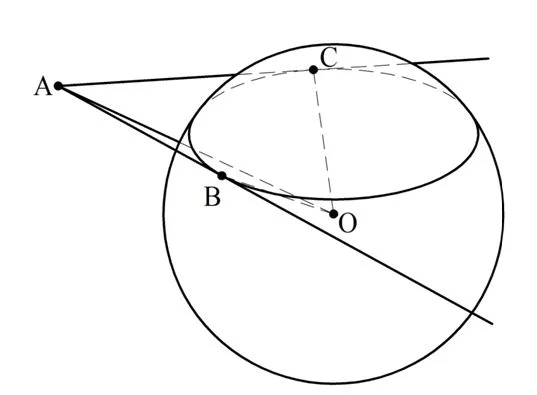
Докажем, что эти отрезки одинаковы. Для этого к точкам касания проведем радиусы ОВ и ОС. Теперь сравним ∆АВО и ∆АСО. Они прямоугольные, ведь ОВ⊥АВ по свойству касательной, и ОС⊥АС. Гипотенуза АО у этих треугольников общая, а катеты ОВ и ОС – это одинаковые радиусы. Получается, что ∆АВО и ∆АСО равны, а потому отрезки АВ и АС одинаковы.

Задание. Дан шар радиусом 10 см, к которому проведена касательная плос-ть α. Через точку касания проведена секущая плос-ть β, образующая с α угол в 30°. Вычислите площадь сечения шара плос-тью β.

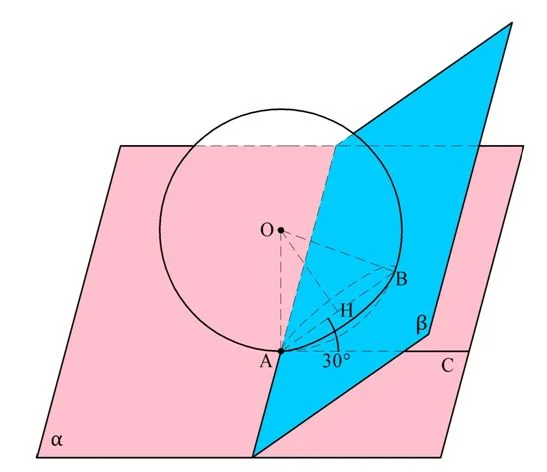
Решение. Обозначим точку касания как А. Опустим из центра сферы о перпендикуляр ОН на плос-ть β. Тогда отрезок АН будет радиусом сечения. Так как угол между плос-тями α и β составляет 30° (на рисунке он показан как ∠НАС), то

Ответ: 25π см2.

Задание. Некоторое тело представляет собой шар, внутри которого есть полость, также имеющая форму шара, причем центры этих шаров совпадают. Докажите, что площадь сечения этого тела, проходящего через центр шаров, совпадает с площадью сечения, являющегося касательной к внутреннему шару.

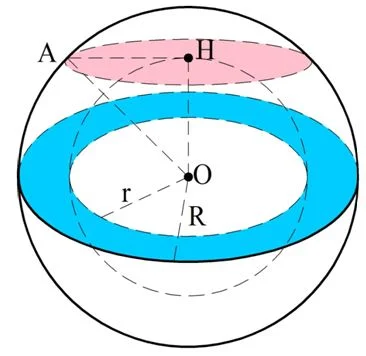
Решение. Обозначим радиус большей сферы как R, а радиус меньшей (внутренней сферы) как r. Площадь центрального сечения в виде кольца (показано синим цветом) представляет собой разницу между площадью большого круга с радиусом R и малого с радиусом r:

Задание. Сфера радиусом 5 см касается каждой стороны треугольника со сторонами 13, 14 и 15 см. Каково расстояние между центром этой сферы и плос-тью треугольника?

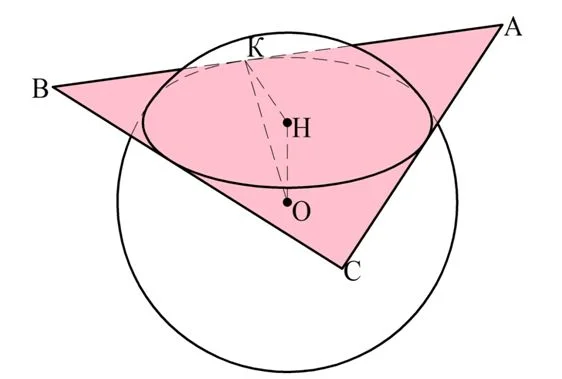
Решение. Обозначим вершины треугольника точками А, В и С. Пусть

AB = 13

AC = 14

BC = 15

Заметим, что плос-ть АВС – секущая, а само сечение имеет форму окруж-ти. Эта окруж-ть будет касаться сторон ∆АВС, то есть она является вписанной окруж-тью. Как вычислить ее радиус НK?

Напомним одну из формул для расчета площади треугольника:

Площадь ∆АВС можно найти по формуле Герона. Предварительно найдем полупериметр ∆АВС:

Что такое сектор?

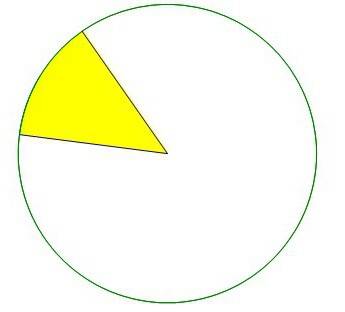
Сектор – это участок круга, который образуется двумя проведенными по нему радиусами. Чтобы понять это определение, нужно просто вспомнить пиццу. Когда ее разрезают на равные кусочки, все они и являются секторами круга, который представлен в виде такого вкусного блюда. При этом совершенно необязательно секторы должны быть равны. Они могут быть разной величины. Например, если отрезать половину пиццы, то она также будет сектором этого круга.

Предмет, отображаемый этим понятием, может иметь только круг. тоже можно провести, конечно, но после этого она станет кругом) не имеет площади, поэтому и сектор выделить не получится.

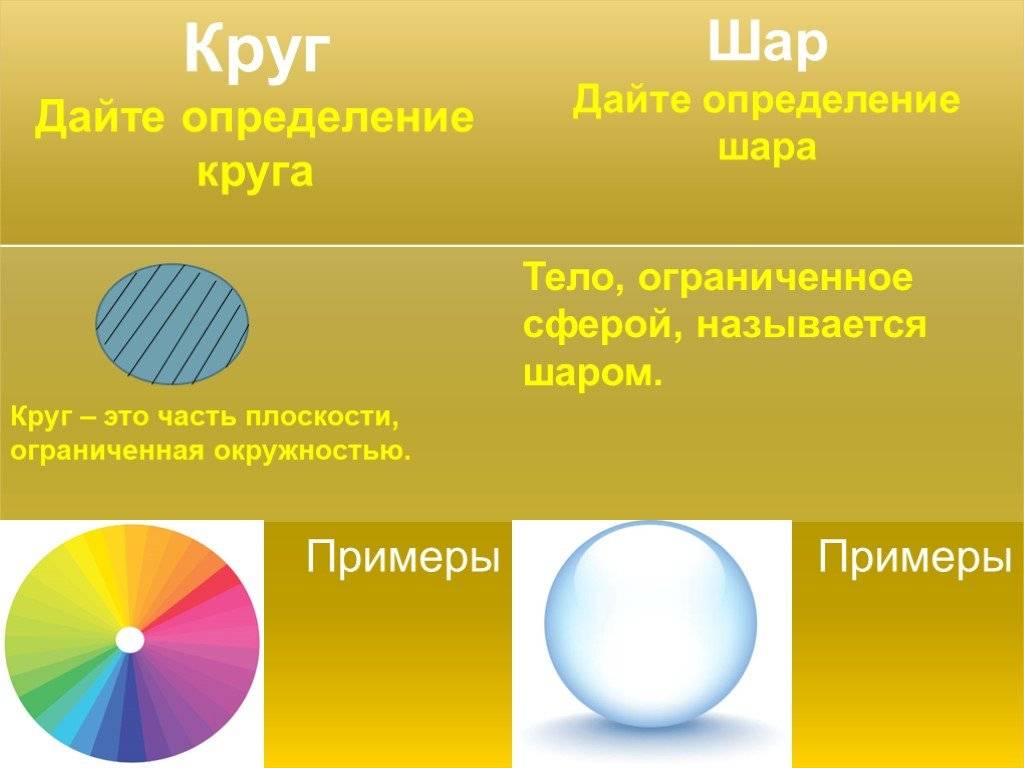
Определение и визуальные отличия

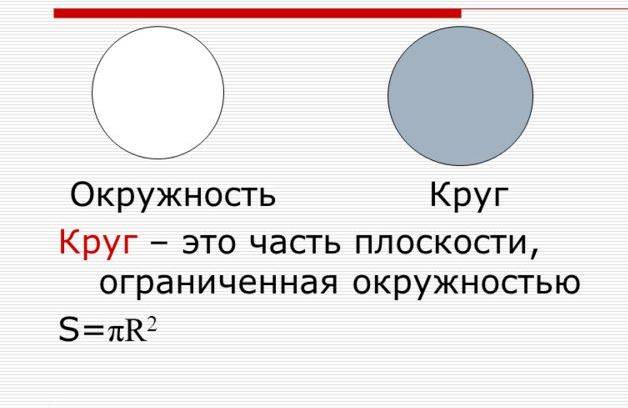
Круг — это плоская фигура, состоящая из всех точек на плоскости, которые находятся на равном расстоянии от одной и той же точки, называемой центром круга. Круг не имеет граней, углов и вершин, он представляет собой замкнутую линию, называемую окружностью.

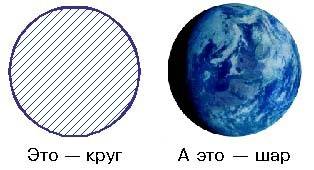
Шар, с другой стороны, является трехмерной фигурой. Он состоит из всех точек в пространстве, которые находятся на равном расстоянии от одной и той же точки, также называемой центром шара. Шар имеет сферическую форму и не имеет ребер, граней и вершин.

Визуально круг выглядит как плоская окружность, в то время как шар имеет объемную форму, похожую на трехмерную окружность.

Основные отличия между кругом и шаром:

Круг — двумерная фигура, шар — трехмерная;
Круг имеет только длину окружности, шар имеет объем и поверхность;
Круг имеет одну характеристику — радиус, шар имеет три характеристики — радиус, площадь поверхности и объем;
Круг может быть нарисован на плоскости, шар может быть изображен в трехмерном пространстве;
Круг используется в геометрии и математике, шар часто используется в физике и геометрии.

Видимые различия

Форма: Основное отличие между кругом и шаром заключается в их форме. Круг представляет собой плоскую фигуру, которая имеет всюду одинаковое расстояние от своего центра до края. Шар, с другой стороны, является трехмерным объектом, имеющим форму полной сферы. То есть, все точки на его поверхности равноудалены от его центра во всех направлениях.
Размеры: Круг может иметь любой радиус, начиная от нуля. Это значит, что круг может быть как очень маленьким, так и очень большим. Шар также может иметь разные размеры, однако его размер определяется не только радиусом, но и его объемом.

Однако, несмотря на эти визуальные различия, круг и шар имеют много общих свойств и характеристик.

Вид сверху

1. Круг является плоской фигурой без изогнутых углов.

2. Все точки на окружности круга равноудалены от его центра.

3. Круг имеет только одну ось симметрии, проходящую через его центр.

Свойства круга:

1. Характерными свойствами круга являются его диаметр и радиус.

2. Диаметр круга — это отрезок, соединяющий две противоположные точки на его окружности и проходящий через его центр.

3. Радиус круга — это отрезок, соединяющий центр круга с любой точкой на его окружности.

Шар — это трехмерное тело, которое обладает следующими характеристиками:

1. Шар является объемной фигурой с плавными кривизнами и без углов.

2. Все точки на поверхности шара равноудалены от его центра.

3. Шар имеет множество осей симметрии, проходящих через его центр.

Свойства шара:

1. Характерными свойствами шара являются его радиус и диаметр.

2. Радиус шара — это отрезок, соединяющий центр шара с любой точкой на его поверхности.

3. Диаметр шара — это отрезок, соединяющий две любые точки на его поверхности и проходящий через его центр.

Круг в реальной жизни

В реальности можно без особых усилий отыскать множество предметов, по форме тождественных кругу. К примеру, готовый образец круга – а, точнее, множество, — каждый день катается по дорогам поселков и городов. Понятно, что речь идет о колесе. Здесь стоит оговориться: круг не должен быть однотонным, это не обязательно. Он может быть украшен узорами или чем-то еще – от этого форма не изменяется.

Колесо

Другой пример круга – Солнце. Да, то самое дневное светило, которое люди лицезреют каждый день. Любознательный читатель заметит, что Солнце – фигура объемная, она не может быть кругом. Это правда. Но маленькая фигура, какой предстает огненная звезда жителям Земли – по сути своей именно круг. Площадь его, конечно, высчитать не получится. Почему? Потому что этот пример приводится только для наглядности, для того, чтобы понять, что такое круг.

Солнце

Определение

Шар
– совокупность всех точек пространства. Все эти точки находятся от центра геометрического тела на расстоянии, которое не больше заданного. Само данное расстояние называется радиусом. Шар, как геометрическое тело, образуется следующим образом: происходит вращение полукруга возле его диаметра. Что касается сферы, то это и есть поверхность шара (например, замкнутый шар включает ее, открытый – нет). Вычисление площади или объема шара – это целые геометрические формулы, которые очень сложны, несмотря на кажущуюся простоту самой геометрической фигуры.

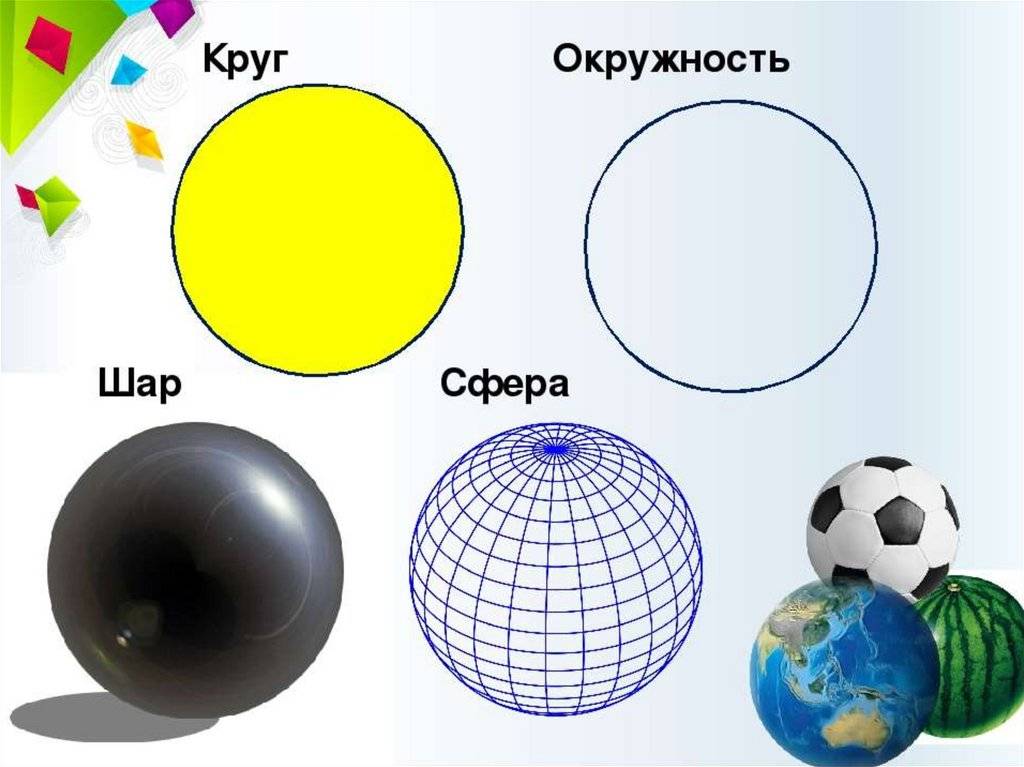
Сфера
, как было отмечено выше, представляет собой поверхность шара, его оболочку. От центра сферы все точки в пространстве равноудалены. Что касается радиуса геометрического тела, то им называют любой отрезок, одна точка которого – непосредственно центр сферы, а другая может находиться в любой точке на поверхности. Можно сказать, что сфера является оболочкой шара без какого-либо содержимого (более конкретные примеры будут приведены ниже). Также как и шар, сфера является телом вращения. Кстати, многие также задаются вопросом, чем же отличаются круг и окружность от сферы и шара. Здесь все просто: в первом случае это фигуры на плоскости, во втором – в пространстве.

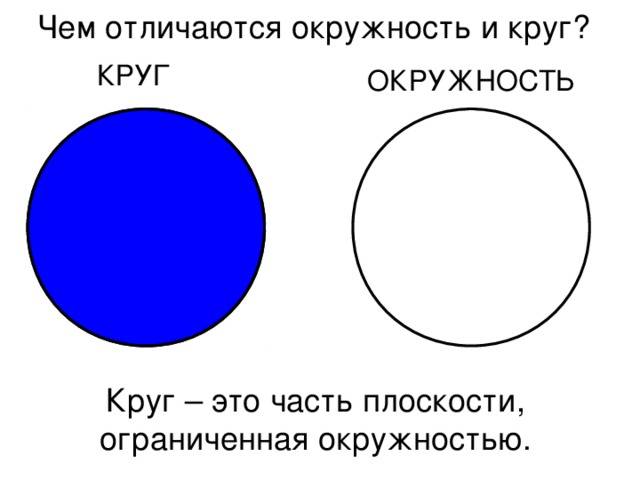
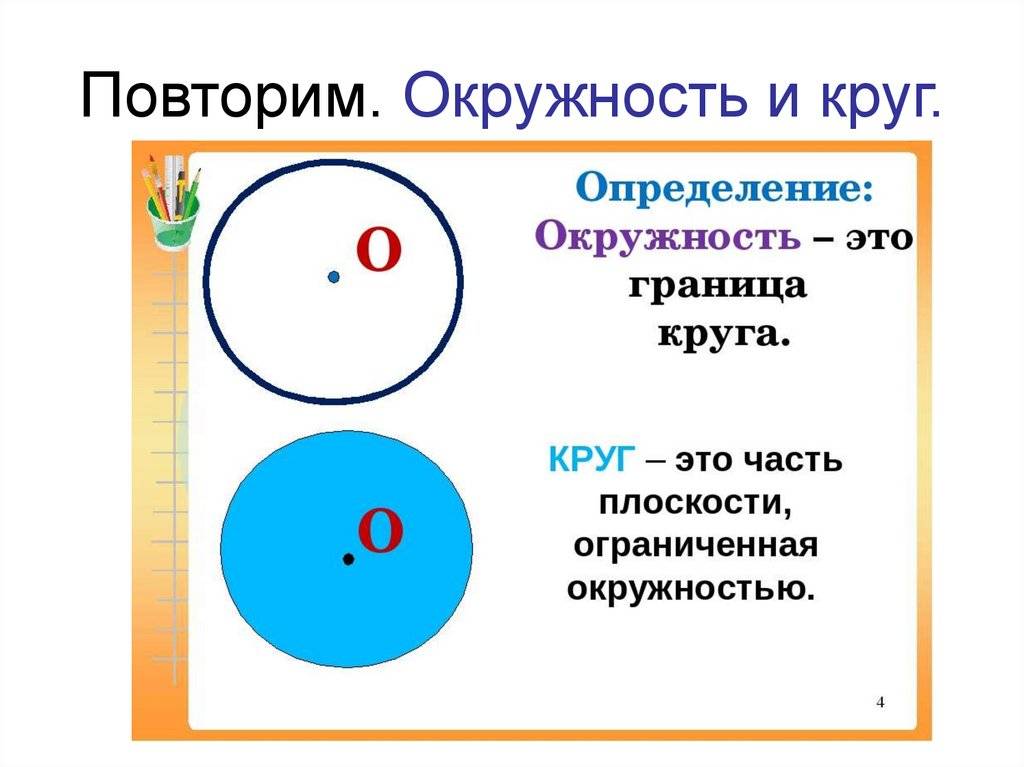
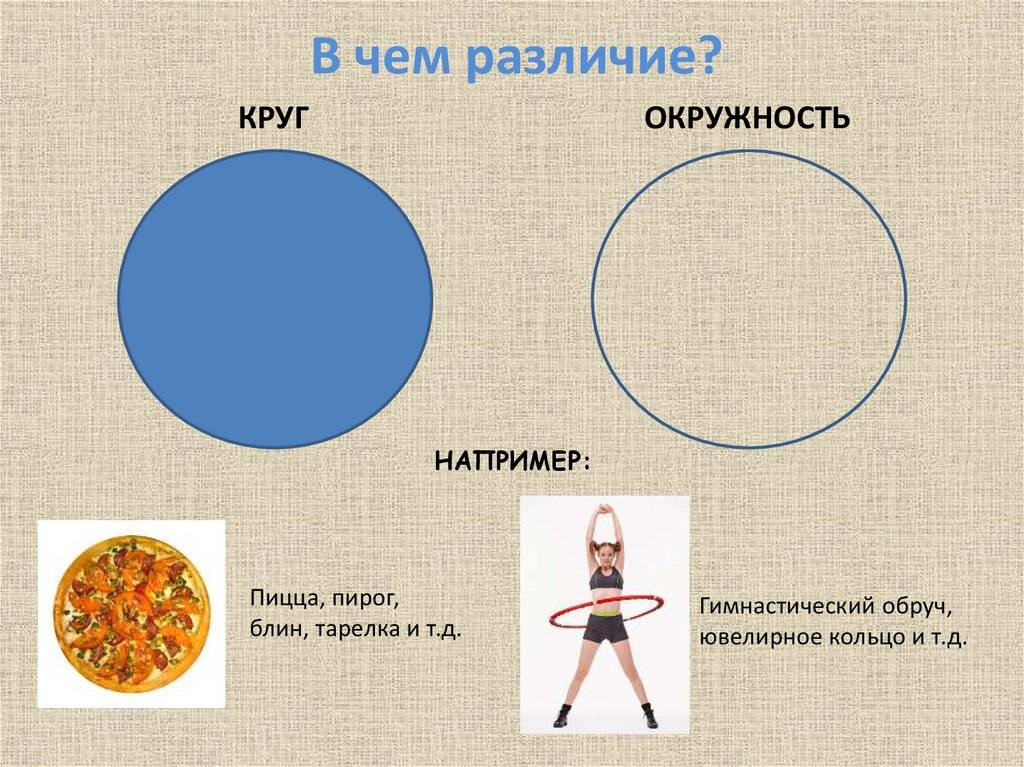
Чем круг отличается от окружности: объяснение

Основное отличие между кругом и окружностью — это то, что круг — геометрическая фигура, а окружность — замкнутая кривая

Также обратите внимание на отличия между окружностью и кругом:

Окружность это замкнутая линия, а круг — площадь внутри этой окружности;
Окружность это кривая линия на плоскости, а круг — пространство, сомкнутое в кольцо окружностью;
Сходство между окружностью и кругом: радиус и диаметр;
У круга и окружности единый центр;
В случае если заштриховывается пространство внутри окружности, оно превращается в круг;
У окружности есть длина, но ее нет у круга, и наоборот, у круга есть площадь, которой нет у окружности.

Публикация «Конспект ОД по теме „Сравнение плоскостной и объёмной фигур, Круг и шар“ (средняя возрастная группа)» размещена в разделах

Геометрические фигуры. Конспекты занятий по математике
Конспекты занятий. Все конспекты
Средняя группа
Темочки
Конкурс для воспитателей и педагогов «Лучший конспект занятия (НОД)» март 2016

-Правильно, а на какую геометрическую фигуру похоже колесо? (Круг). Колесо поможет нам разгадать загадки круга.

– Чтобы отправиться в путешествие, нам нужно вырезать круг из бумаги. Берите ножницы- и за дело! (воспитатель знакомит детей с техникой безопасности при работе с ножницами).

– У вас получились отличные круги. Назовите предметы, которые похожи на ваш круг. (Руль, тарелка, часы, блин, пуговица).

– А теперь поиграем с кругом : покатайте его (получается, спрячьте в ладошку (получается). Почему у вас это получилось? (он маленький). Да, но самое главное- он не толстый, а ровненький.

– Такие фигуры называются плоскими. Повторим хором – это новое слово: (плос- ки- ми).

– Ребята, мы не сможем поехать дальше, пока не приклеим наши колёса на автобус.

-Молодцы, все справились!

А теперь нас ждёт следующее задание, вы с закрытыми глазами, должны наощупь найти геометрическую фигуру, похожую на колесо. Это будет вашим билетом. (Дети с завязанными глазами отыскивают на подносе фигуру «круг»).

– Как называется эта фигура? (Круг). Ребята вы отлично справились и с этим заданием.

– Мы отправляемся к новой станции «Угадай – ка».

2.2 Добывание нового знания.

2 станция «Угадай- ка»

– На станции нас ждёт таинственный мешок – откроем его. Ребята найдите среди этих игрушек (кубик, конус, цилиндр, 6 мячей и т. д.) похожий на круг.

– Назовите предметы, которые похожи на шар (апельсин, арбуз, мяч, лампа, помидор).

– Молодцы! Давайте посчитаем, сколько у нас мячей (считают хором до пяти).

– Поиграем с мячиком: покатайте его вперёд, покатайте его назад, покатайте его вокруг себя). Получается? Почему? (Он круглый, надутый).

Такие фигуры называются объёмными. Повторим хором – это новое слово: (объ- ём- ный).

– Что общего у этих мячей? (Они круглые, объёмные).

– А чем они отличаются? (Они разные по цвету).

– А теперь попробуйте закрыть мячик ладошками. Получается? Почему не получается? (Он большой, круглый, надутый, объёмный).

Вы замечательно справились с заданием. Дальше отправляемся в путь.

3 станция «Поиграй- ка»(Физминутка)

Встав в круг, дети передают свой мяч товарищу справа, который получит его только в ответ на просьбу «Дай, пожалуйста» и поблагодарит «Спасибо». Начинает игру воспитатель со словами: «Дай, пожалуйста, мячик».

– А теперь послушайте стихотворение и повторяйте мои движения:

Раз, два, три, четыре, пять-

Любит мячик поскакать.

Я за мячиком лечу-

Удержать его хочу. (Дети прыгают с мячом, потом делают 3 удара им об пол).

2.3 Самостоятельная деятельность детей по закреплению нового знания (Исследование).

4 станция «Искупай- ка».

– А вот и 3 станция «Искупай- ка».

– На столе вырезанные из бумаги круги и шары. Попробуем «искупать» их: положите круги в воду, опустите на дно.

– Что с ними произошло? (Они утонули). Почему это произошло (Они бумажные, мокрые).

– Попробуем «искупать» мячики, опустив их в воду. Что с ним происходит? (Он не тонет, выпрыгивает).

– Почему мяч не тонет? Что у него внутри? (Воздух).

– Верно, он объёмный, не тонет, потому что у него внутри воздух.

III. Заключительная часть. Анализ и самоанализ деятельности детей.

5 станция «Повторяй- ка»

– Следующая станция «Повторяй- ка». Нужно вспомнить, с какими фигурами мы играли? (Круг, шар).

– Что нового вы узнали про круг и про шар? Я начну, а вы продолжите мои слова, поможете мне.

– Мы узнали, что круг (какой?- … плоский или объёмный). Мы узнали, что шар (какой?-… плоский или объёмный).

Сюрприз «Весёлый салют!»

– Вы прекрасно справились со всеми заданиями. Поэтому вас ожидает сюрприз.

– Что это? (Мыльные пузыри). Почему мы выбрали именно пузыри? (Потому что они похожи на шарики). Сделаем салют из мыльных пузырей. Чей салют будет самый красивый?

– У нас получился большой салют. А мыльные пузыри- в подарок вам за весёлое путешествие.

Примеры круга в реальной жизни

На самом деле возможных предметов, которые можно назвать разновидностью круга, достаточно. Например, если посмотреть на колесо машины прямо, то вот вам пример готового круга. Да, он необязательно должен быть заполнен однотонно, вполне возможны различные узоры внутри него. Второй пример круга – это солнце. Конечно, на него посмотреть будет тяжело, но оно на небе выглядит, как маленький кружочек.

Да, сама звезда Солнце – это не круг, она имеет еще и объем. Но вот само солнце, которое мы видим над нашей головой в летнее время, является типичным кругом. Правда, площадь у него все равно высчитать не получится. Ведь сравнение его с кругом приводится только для наглядности, чтобы было проще понять, что такое окружность и круг.

Небольшое погружение в один из разделов математики

Для начала потребуется вспомнить о существовании науки геоме́трии (в несколько вольном переводе с греческого это слово означает «землемеренье») — обособленном разделе математики, специализирующемся на изучении пространственных структур, их отношений между собой и различных возникающих из этого обобщений

Важно, что несмотря на подобное «приземлённое» происхождения названия эта наука оперирует сугубо абстрактными понятиями, которые в привычном нам мире не существуют в прямом физическом воплощении

Одно из таких базовых понятий — это геометрическая точка
. Напрягите своё воображение: в отличие от «точки карандашом», «точки от булавки» и так далее эта точка представляет из себя полностью абстрактный объект в воображаемом пространстве без каких-либо измеримых характеристик типа «толщины», «цвета» и так далее (математики любят при этом произносить словосочетание «нульмерный объект»). В принципе, всё остальное в геометрии будет далее определяться исходя именно из этой абстракции.

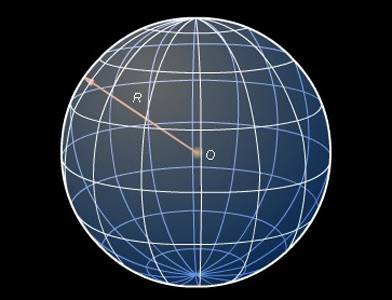
Следующее нужно для дальнейших рассуждений понятие — это «ритуальная» математическая фраза «геометри́ческое ме́сто то́чек» (ГМТ). C её помощью описывается некоторое множество (совокупность) точек, подпадающих под определённое отношение (свойство) — таким образом задаётся «геометрическая фигура». Пример: сфе́ра (от древнегреческого σφαῖρα, изначально обозначающего мяч/шар) — это геометрическое место таких точек пространства, которое можно описать как равноудалённое (находящееся на строго одном расстоянии) от некоторой заданной точки, обычно называемой «центром сферы».

Расстояние же от центра сферы до этого ГМТ принято называть «радиусом сферы»

Во время всех этих манипуляций важно продолжать помнить, что сфера — понятие более эфемерное, чем даже всем привычный и знакомый мыльный пузырь: у любого мыльного пузыря всё-таки есть вполне ощутимая стенка из водно-мыльной плёнки микроскопической толщины, которую можно физически измерить (и даже проткнуть), а у сферы — нет!

Теперь обратимся к определению шара: под шаром понимается совокупность всех таких точек пространства, что находится от определённой точки (центра шара) на расстоянии, не большем заданного (радиуса шара). Иначе говоря, шар является «геометрическим телом» — тем, что согласно первичному определению Евклида «имеет длину, ширину и глубину» (в современных учебниках это определение менее наглядно: «часть пространства, ограниченная своей образуемой формой»).

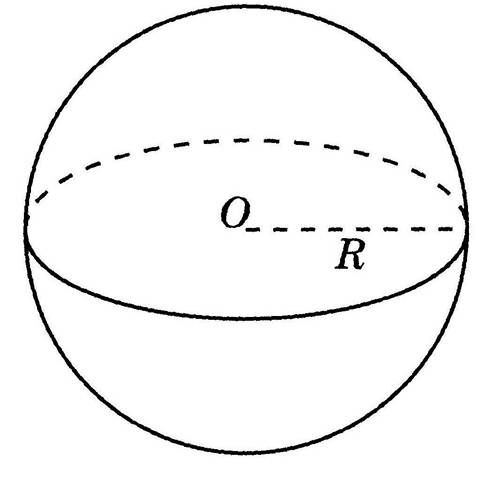
Попутно отметим, что использованные здесь способы задания сферы и шара через центр и радиус — не единственные: например, задание сферы/шара в пространстве можно выполнить посредством вращения окружности, круга и т.д. (глубоко заинтересовавшимся этим вопросом настоятельно рекомендуется ознакомиться с отдельным разделом геометрии под названием «Фигуры и тела вращения», поскольку это часто применяемый способ задания самых различных геометрических фигур и тел в пространстве).

Таким образом, и в случае сферы, и в случае шара приходится иметь дело с определённым образом заданным геометрическим местом точек (то есть геометрической фигурой), однако лишь в случае шара можно говорить о геометрическом теле. Любопытно отметить, что строго говоря сферу из шара можно «вычесть»: в этом случае математики говорят об «открытом шаре». Однако «по умолчанию» имеет место «замкнутый шар», где сфера является его естественной границей и принадлежащей ему частью.

Отличия окружности от круга

Значит, какой вывод мы можем сделать? Чем отличается окружность от круга, так это тем, что у последнего есть площадь, и в большинстве случаев окружность является границей круга. Хотя бывают и исключения на первый взгляд. Может показаться иногда, что нет окружности в круге, но это не так. В любом случае что-то да есть. Просто окружность может быть очень маленькой, и тогда ее не видно невооруженным глазом.

Также окружностью может быть то, что выделяет круг из фона. Например, на приведеном выше изображении синий круг находится на белом фоне. А вот та черта, по которой мы понимаем, что здесь начинается фигура, и называется в данном случае окружностью. Таким образом, окружность – круга. Вот чем отличается окружность от круга.

Обучение формам и цветам

Однако, перед тем как начать обучение, необходимо научиться различать базовые геометрические формы, такие как круг, квадрат, треугольник и прямоугольник. Для начала можно использовать разные игрушки или картинки, чтобы ребенок мог узнать и называть эти формы.

Цвета также играют важную роль в развитии ребенка. Они помогают улучшить зрительное восприятие и способность определить объекты вокруг себя. Для начала можно использовать разноцветные игрушки или карточки с изображениями, чтобы ребенок мог учиться называть цвета и распознавать их.

Когда ребенок уже знает основные формы и цвета, можно углубить знания, предлагая ему задания, связанные с соответствием формы и цвета. Например, показывая ребенку разные объекты разных форм и цветов, можно попросить его выбрать объект определенной формы или цвета.

Обучение формам и цветам также можно проводить с помощью игр и развивающих упражнений. Ребенок может собирать разные формы из конструктора или раскрашивать рисунки разными цветами

Важно, чтобы обучение проходило в игровой форме, чтобы ребенок был заинтересован и вовлечен в процесс

Таким образом, обучение формам и цветам помогает развивать мозговые навыки, улучшает зрительное восприятие и помогает строить понимание окружающего мира

Важно проводить обучение в игровой форме, чтобы ребенок был заинтересован и мог активно участвовать в процессе обучения

Что такое круг?

Начертание круга начинается с окружности. Окружность – это замкнутая черта без конца и начала
, каждая точка которой находится на равном удалении от центра. Простейший пример окружности – гимнастический обруч.

Круг получится, если начертить окружность, например, на бумаге – и потом разукрасить ее. Любыми красками: желтой, синей, зеленой – какая больше нравится. Главное – заполнить чем-то пустоту. После окончания работы окружность превратится в фигуру, которую именуют кругом. Круг по сути своей – это некоторая часть двухмерной поверхности, закольцованная в окружность.

Круг обладает некоторыми важными для понимания его сущности параметрами. Кстати, часть данных параметров присуща и окружности.

Радиус
– расстояние от центральной точки круга или окружности до границы фигуры (линии, которая ее очерчивает).
Диаметр
– важная характеристика, которая так часто фигурирует в школьных заданиях. Это сумма двух радиусом, то есть расстояние между двумя противоположными точками на окружности.
Площадь
– свойство, характерное только для круга. Окружность не имеет его в силу своей структуры (потому что она пустая, а центр фигуры – воображаемая точка). В круге, напротив, несложно определить центр. Через центральную точку фигуры достаточно просто прочертить ряд линий, которые поделят круг на сектора.

Свойства круга и шара

Окружность – это геометрическая фигура, представляющая собой границу, образуемую всеми точками на плоскости, равноудаленными от одной точки, называемой центром окружности. Форма окружности является плоской и имеет конечный диаметр, радиус и длину окружности, которая вычисляется по формуле.

Шар, в отличие от окружности, является трехмерным телом, представляющим собой объем, ограниченный поверхностью, состоящей из всех точек пространства, равноудаленных от одной точки, называемой центром шара. Поверхность шара является сферой и имеет конечную площадь, радиус и объем, которые могут быть вычислены по соответствующим формулам.

Таким образом, основное отличие между кругом и шаром заключается в их размерности и форме. Круг ограничен плоской границей на плоскости, в то время как шар ограничивается трехмерной сферической поверхностью в пространстве.

Кроме того, у круга и шара есть и другие характеристики, такие как диаметр, радиус, площадь и объем, которые используются для вычисления и определения их свойств и параметров.

Площадь

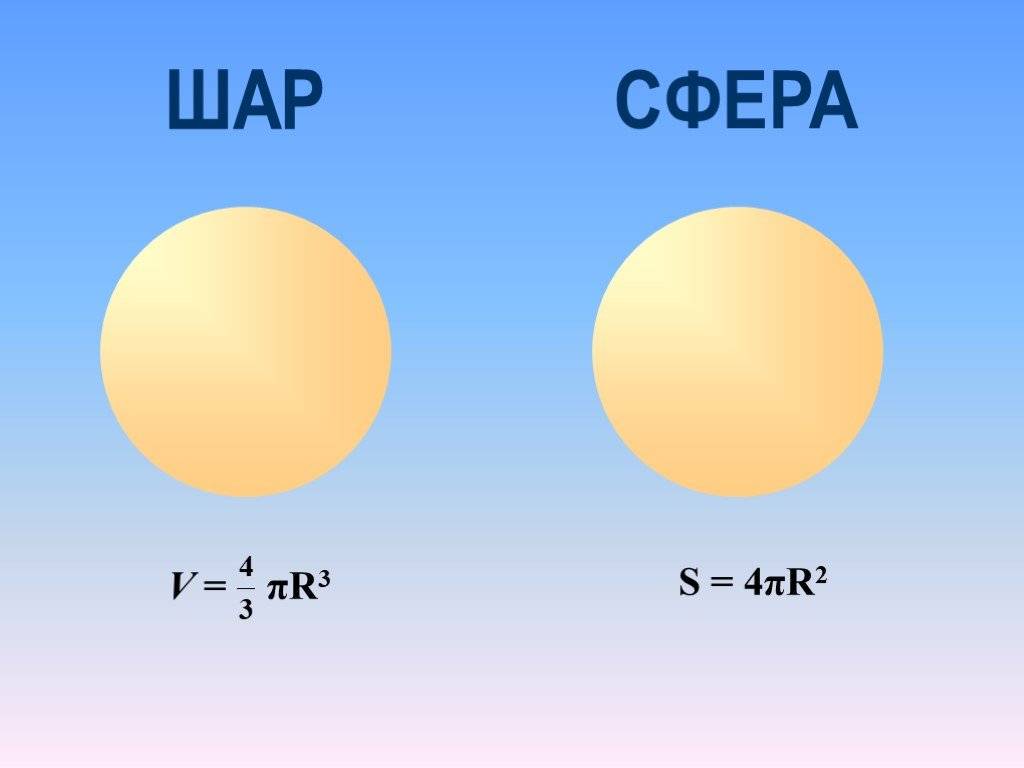
Круг — это геометрическая фигура, которая лежит на плоскости и ограничена окружностью. Площадь круга вычисляется по формуле S = πr^2, где π — математическая константа, равная примерно 3,14159, а r — радиус окружности.

Шар — это тело, имеющее форму сферы, которая не лежит на плоскости. Площадь поверхности шара вычисляется по формуле S = 4πr^2, где π — математическая константа, равная примерно 3,14159, а r — радиус сферы.

Таким образом, площадь круга и площадь поверхности шара различаются как по формулам вычисления, так и по границам, на которых они лежат — круг лежит на плоскости, а шар — на границе трехмерного пространства. Круг ограничен окружностью, а шар — сферой.

Помимо площади, у круга и шара есть и другие характеристики, такие как объем — мера пространства, занимаемого фигурой. Объем круга равен нулю, так как круг лежит на плоскости. А объем шара вычисляется по формуле V = (4/3)πr^3, где π — математическая константа, равная примерно 3,14159, а r — радиус сферы.

Длина окружности или окружности большой окружности

В то же время, шар является трехмерным телом, которое ограничено поверхностью, называемой сферой. Сфера — это множество всех точек, равноудаленных от центральной точки, которую мы также называем центром. Шар обладает объемом и поверхностью. Поверхность шара вычисляется по формуле: S = 4πr^2, где S — площадь поверхности шара, r — радиус шара. Объем шара вычисляется по формуле: V = (4/3)πr^3, где V — объем шара, r — радиус шара.

Таким образом, длина окружности является одной из характеристик круга, в то время как объем и площадь поверхности — характеристики шара. Круг и шар имеют различную форму и размерность, однако оба эти объекта имеют схожую геометрическую особенность — центральную симметрию.

Параметр	Круг	Шар
Форма	Плоская	Трехмерная
Граница	Окружность	Сфера
Характеристика	Длина окружности	Площадь поверхности, объем

Объем

Шар имеет форму трехмерного объекта, который состоит из плоскости и точек на ней. Поверхность шара представляет собой сферу, а его граница образует окружность. Чтобы вычислить объем шара, необходимо знать его радиус и использовать формулу, которая связывает радиус и объем.

Круг, с другой стороны, является двумерным объектом, который представляет собой плоскую фигуру. Круг является границей шара и состоит только из окружности. Объем круга не может быть рассчитан, поскольку круг не имеет третьей измерения.

Таким образом, отличие между кругом и шаром в понятии объема состоит в том, что шар имеет объем, а круг — нет.

Основные различия между кругом и шаром

Форма: Круг представляет собой плоскую геометрическую фигуру, которая состоит из всех точек равноудаленных от центра. Он имеет только одну размерность — длину. Шар же является трехмерным объектом, образованным поворотом окружности вокруг ее диаметра. Он имеет три размерности — длину, ширину и высоту.
Граница: У круга есть только одна граница — окружность, которая представляет собой замкнутую кривую линию. Шар же имеет границу, которая является сферой. Сфера ограничивает внутреннее пространство шара и представляет собой поверхность без углов или краев.
Расположение в пространстве: Круг находится на плоскости и не имеет высоты или глубины. Он может быть изображен на бумаге или другой плоской поверхности. Шар же занимает трехмерное пространство и имеет объем. Он может быть представлен в реальном мире, например, как мяч или планета.

Таким образом, круг и шар имеют существенные различия в своей форме, границе и расположении в пространстве. Понимание этих различий поможет вам использовать правильные термины и характеристики при описании и изучении этих геометрических фигур.

Форма

Шар, с другой стороны, имеет трехмерную форму и является геометрическим телом с гладкой поверхностью. Поверхность шара состоит из всех точек, находящихся на одинаковом расстоянии от его центра.

Еще одно отличие между окружностью и поверхностью шара заключается в их границах. Граница окружности представляет собой круглую линию, тогда как граница шара является закрытой поверхностью без острых углов или ребер.

Форма окружности и шара также отличается по объему. Окружность не имеет объема, так как она является плоской фигурой, в то время как шар имеет конечный объем, который можно вычислить с помощью соответствующей формулы.

В заключение, форма является основной характеристикой, которая отличает окружность от шара. Окружность является двумерной плоской фигурой с границей в форме круга, тогда как шар имеет трехмерную форму с границей в форме сферы и объемом.

Размеры

Круг и шар имеют разные формы и границы.

Круг — это фигура, ограниченная окружностью. Окружность — это замкнутая линия, расположенная в одной плоскости.

Шар, в свою очередь, имеет форму трехмерного объекта и обладает поверхностью. Поверхность шара не является плоской, она имеет кривизну.

Главное отличие между кругом и шаром заключается в их размерах. Круг имеет только два размера: радиус и диаметр. Радиус — расстояние от центра круга до любой точки на его окружности. Диаметр — дважды радиус круга, то есть расстояние между двумя точками на противоположных сторонах круга через его центр.

С другой стороны, размеры шара включают не только радиус и диаметр, но и объем. Объем шара — это мера трехмерного пространства, занимаемого шаром.

Размерностные характеристики

Шар, с другой стороны, является трехмерным объектом и имеет объем. Шар также имеет центр, но в отличие от круга, все точки шара находятся на одинаковом расстоянии от центра во всех направлениях, что делает его форму круглой. Шар описывается размерностными характеристиками, такими как радиус и диаметр, где радиус — это расстояние от центра шара до любой точки его границы (поверхности шара), а диаметр — это двукратное значение радиуса.

Выводы сайт

Сфера полая, в то время как шар является заполненным внутри телом. Например, воздушный шар – это сфера, бильярдный шар – это полноценный шар.
Сфера имеет площадь и не имеет объем, шар же наоборот.
Третье отличие – это измерение радиуса двух геометрических тел.

Если взять полукруг или круг и провернуть его вокруг своей оси, получится тело, называемое шаром. Иными словами, шаром называется тело, ограниченное сферой. Сфера представляет собой оболочку шара, и ее сечением является окружность. Шар и сфера — взаимозаменяемые тела, в отличие от конуса, несмотря на то, что конус также является телом вращения. Через две точки A и B, располагающиеся в любом месте поверхности шара, может проходить бесконечное количество кругов или окружностей. Данная формула может быть полезна в том случае, если известен либо диаметр, либо радиус шара или сферы. Однако, эти параметры приведены в качестве условий не во всех геометрических задачах.

Если известна длина диаметра сферы (d), то для нахождения площади ее поверхности (S) возводите этот параметр в квадрат и умножайте на число Пи (π): S=π∗d². Например, при длине радиуса сферы в три метра его площадь составит 4∗3,14∗3²=113,04 квадратных метров. Для вычисления площади сферы по данным, например, из второго шага поисковый запрос, который надо ввести в Google, будет выглядеть так: «4*пи*3^2». А для наиболее сложного случая с вычислением кубического корня и возведением в квадрат из третьего шага запрос будет таким: «пи*(6*500/пи)^(2/3)».